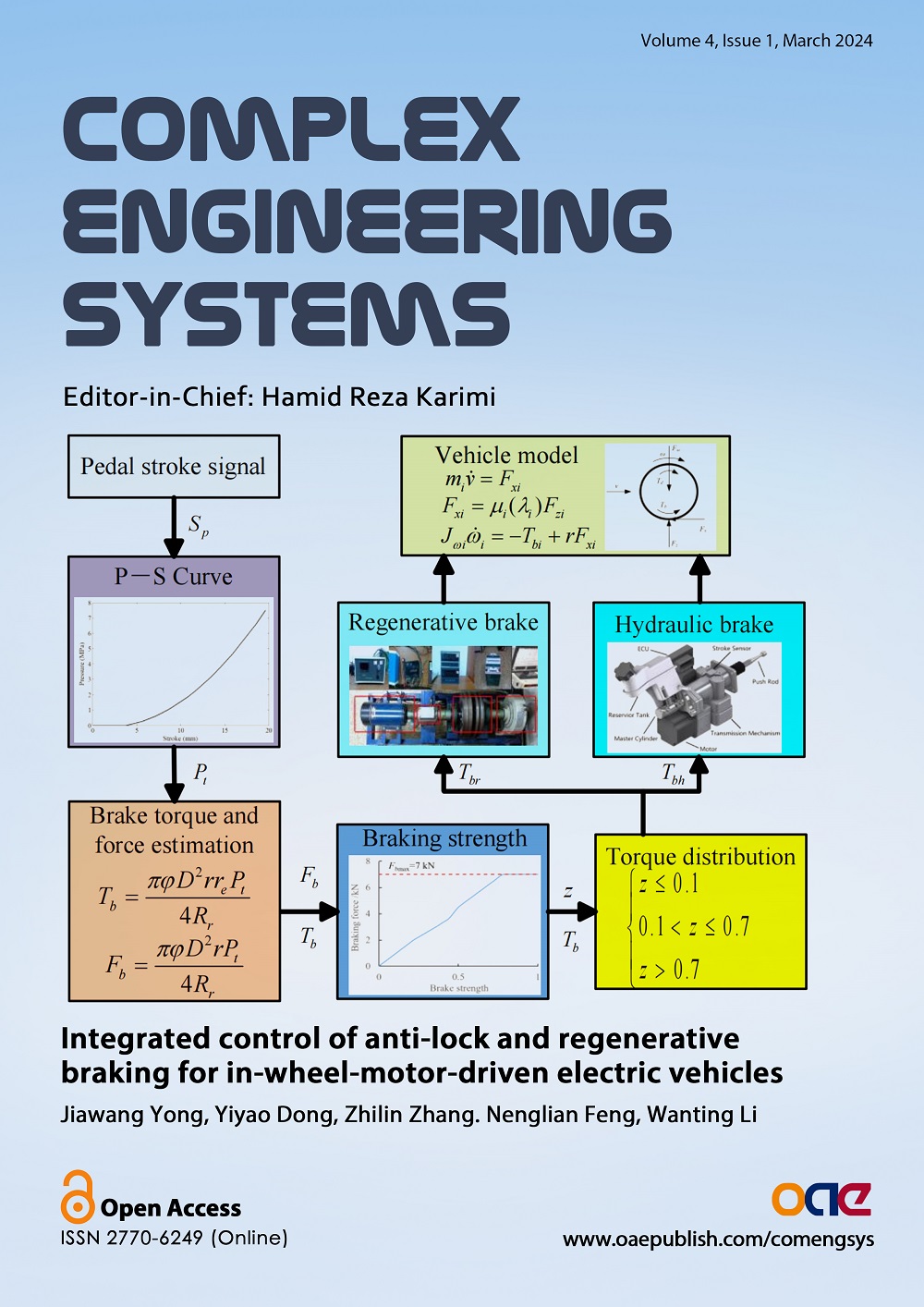
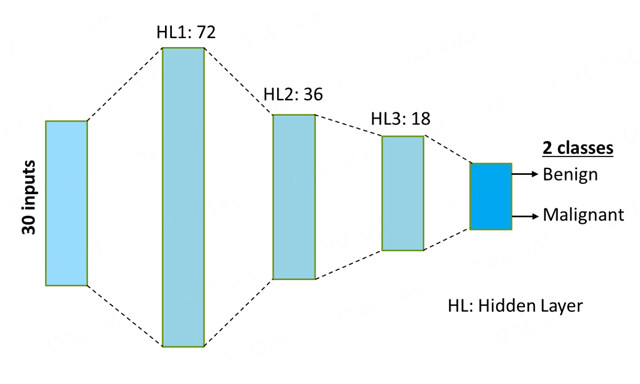
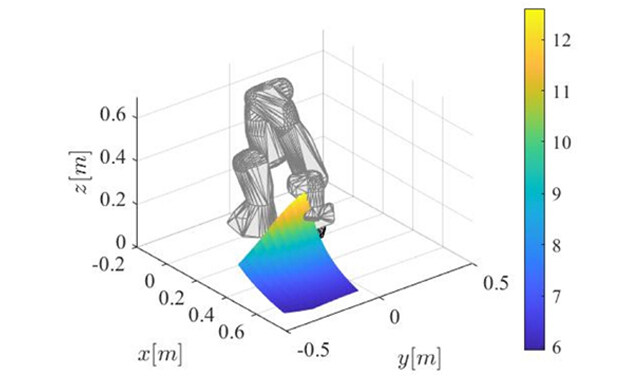
Complex Engineering Systems
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:

Data
200
Authors
275
Reviewers
2021
Published Since
67,500
Article Views
24,811
Article Downloads
For Reviewers
For Readers
Add your e-mail address to receive forthcoming Issues of this journal:
Themed Collections
Related Journals

Related Journals
Data
200
Authors
275
Reviewers
2021
Published Since
67,500
Article Views
24,811
Article Downloads