Research Article | Open Access | 18 Jul 2022

An improved A star algorithm for wheeled robots path planning with jump points search and pruning method

Views: 1415 | Downloads: 644 | Cited:

Hongqian Huang

, ...

Qing Bai

Complex Eng Syst 2022;2:11.

10.20517/ces.2022.12 | © The Author(s) 2022.

Author Information

Article Notes

Cite This Article

Abstract

Wheeled robots enjoy popularity in extensive areas such as food delivery and room disinfection. They can lower labor costs, protect human health from infection, and so on. Given the need to avoid obstacles, the path planning of robots is an elementary module. The A* algorithm has been widely used thus far, but it suffers much memory overhead and provides a suboptimal path. Therefore, we propose an improved A* algorithm with the jump point search method and pruning idea. Specifically, the jump point search method reduces the occupancy rate of the open list. The shorter length of the path can be achieved by pruning. Simulation experiments proved that the improvement was effective and practical.

Keywords

Wheeled robot, A* algorithm, occupancy rate, pruning

Download PDF 0 43

1. INTRODUCTION

In recent years, wheeled robots have gained more and more popularity and have been applied to extensive scenarios ^[1-3]. They can deliver food ^{[4, 5]}, provide security guards ^{[6, 7]}, and offer services ^{[8, 9]} for people. Path planning for wheeled robots ^[10-12] is one of the hottest and most difficult spots in robot research. The existing path planning methods are mainly divided into three categories: graph-based, sampling-based, and intelligent methods. Traditional graph-based search methods include A* ^{[13, 14]}, LPA* ^{[15, 16]}, ARA* ^{[17, 18]}, etc. Sampling-based search methods include RRT ^{[11, 19]}, RRT* ^{[20, 21]}, RRT-Connect ^{[22, 23]}, etc. Intelligent methods include particle swarm algorithm ^[24], genetic algorithm ^[25], ant colony algorithm ^[26], etc. The A* algorithm is a global path planning method based on known environmental information, with a real-time and better suboptimal solution, thus it has been widely employed.

However, the classical algorithm has the disadvantages of much memory overhead and providing a suboptimal solution. Therefore, some researchers have proposed to improve the A* algorithm. For the purpose of stability and effectiveness, Wang et al.^[27] presented the improved method from the view of expansion distance, bidirectional search, heuristic function optimization, and smoothing. Song et al.^[28] considered the cost function with an additional parameter, with the result of fewer nodes and lower memory overhead. Specifically, the parameter is a cost from the previous point to the final one. Zhang et al.^[29] achieved a high success rate and short length through applying an early-stop method, in which the local path is used directly if it is safe and collision-free. In addition, they also introduced a post-processing stage to shorten the resulting path by straightening the local path.

Under the environmental model, grid map, this paper proposes an effective method of global path planning for wheeled robots. First, we analyze the shortcomings of the A* algorithm and find a corresponding measurement. To solve the problem of excessively high node occupancy rate of open list, a jump point search method is adopted ^{[30, 31]}. Only the nodes with special properties are added to the open list during the process of node expansion. Considering the suboptimal solution of the path, a pruning method is proposed based on the axiom that the shortest path between two points is a straight line ^[32]. The polyline with an inflection point is replaced by a straight line. Lastly, a C++ simulation was designed and performed to verify that the improved A* algorithm can improve the traditional one.

The rest of this paper is structured as follows. In Section 2, we review the traditional A* algorithm for path planning. In Section 3, we propose the idea of combining jump search and pruning to improve the A* algorithm. Experimental results are shown in Section 4. Finally, this paper is summarized in Section 5.

2. TRADITIONAL A* ALGORITHM

2.1. Grid map

In this paper, the map used in path planning is the grid map ^[33], which is a common map representation. The basic idea is to decompose the environment into local units, i.e., grid, and assign the state of occupancy to each grid. If there is an obstacle located in the grid, then it is a non-free grid, which is inaccessible to the robot. Otherwise, it is reachable, called a free grid. To simplify the path planning process of wheeled robots, we set up the following assumptions:

Assumption 1: In the process of planning a feasible path, the size and position of the obstacles remain static.

Assumptions 2: In the process of planning a feasible path, the obstacle can occupy the grid completely.

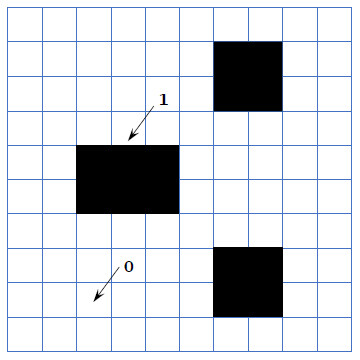
In this work, we use the evenly spaced grids and assume 1 denotes the non-free grid and 0 denotes the free grid, as shown in Figure 1.

An improved A star algorithm for wheeled robots path planning with jump points search and pruning method

Figure 1. Occupancy state of the grid map.

2.2. A* algorithm

Based on the known grid, the A* algorithm mainly plans the path and applies an evaluation function to determine its expansion direction. The function represents the distance between the initial node and target node by the expansion one. The equation of the evaluation function is defined as follows:

(1)

$$ \begin{equation} f(n)=g(n)+ h(n) \end{equation} $$

where $$g(n)$$ represents the actual distance from the initial node to the current node in the grid map, and $$h(n)$$ represents the Manhattan distance of the optimal path from the current node to the target node. The closer the Manhattan distance is, the more optimal the feasible path is. A* algorithm starts the searching from the initial node to eight neighbor nodes and expands successively with equal probability, as shown in Figure 2

Figure 2. Node expansion in equal probability.

Then, a node expansion or searching process based on the minimum value continues. First, the values of each node of the surrounding eight neighbor points are estimated. Second, the node with free grid with the lowest estimated value is selected, which is set as the starting node in the next expansion process. Third, the chosen node is added to the open list and the node with the minimum value in the open list is chosen for the closed list. The expansion terminates when the target node is visited. During the process above, the distance between two nodes is obtained by the Manhattan distance:

(2)

$$ \begin{equation} d = \left|x_1-x_2\right| + \left|y_1-y_2\right| \end{equation} $$

where $$(x_1, y_1)$$ and $$(x_2, y_2)$$ represent the coordinates of the two nodes $$n_1$$ and $$n_2$$, respectively, and $$d$$ represents the estimated distance between the two nodes.

If $$g(n)$$ is equal to zero, the A* algorithm becomes the best optimal search with a greedy strategy for the expansion of nodes. The search time is shortened but at the cost of a suboptimal solution. If $$h(n)$$ is equal to zero, the A* algorithm becomes Dijkstra's algorithm with the requirements of exploring all directions. Although it results in the optimal solution, it uses a lot of computation resources. When terms of $$g(n)$$ and $$h(n)$$ are non-zero, relatively optimal solution and real-time performance are both guaranteed.

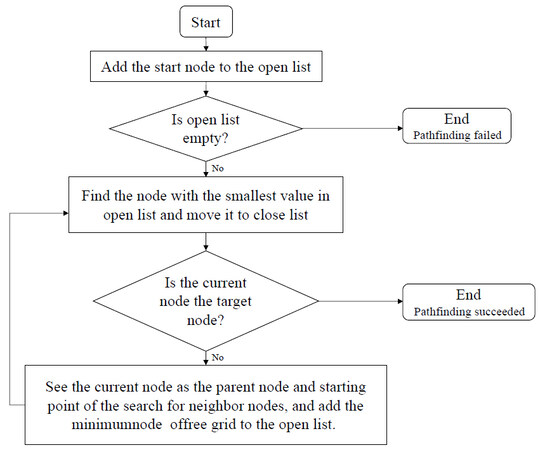
Besides, we note that two node containers, named open list and closed list, respectively, are built. The generated nodes in the expansion are stored in the open list and the nodes with minimum value in the open list are stored in the closed list. After the planning process, a suboptimal path is generated. The flow chart of A* is shown in Figure 3.

Figure 3. Flow chart of traditional A* algorithm.

The specific steps of the A* algorithm are as follows.

Step 1: Initialize the grid map and define the search method of nodes to expand neighbor nodes in sequence with equal probability.

Step 2: Add the initial node to the open list.

Step 3: Determine whether the open list is empty. If it is true, the pathfinding fails. Otherwise, continue to Step 4.

Step 4: Find the node with the smallest value in the open list and move it to the closed list.

Step 5: Determine whether the current node is the target node. If it is true, the pathfinding is successful. Otherwise, continue to Step 6.

Step 6: Consider the current node as the parent node and starting point of the search for neighbor nodes and add the minimum node of the free grid to the open list. Continue to Step 4.

In the next section, we discuss how to improve the A* algorithm.

3. IMPROVED A* ALGORITHM

Given the high node occupancy rate and suboptimal solution, the jump points search and pruning methods are used to improve the A* algorithm.

3.1. Selective strategy

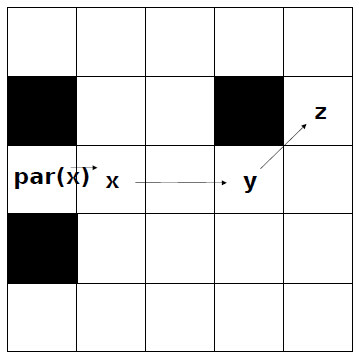
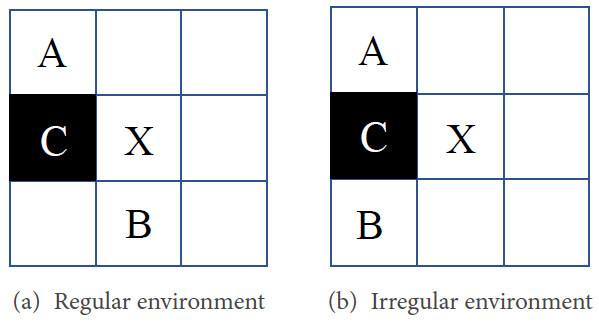
In this section, a selective node search strategy is developed. Only the node with specific properties can be chosen. An example of selective strategy is shown in Figure 4. Specifically, there is a neighbor node of the node $$par(x)$$ with the direction from left to right. It is valueless to further search along the direction for the least cost of the distance between $$par(x)$$ and $$x$$. In other words, there is no need to add these corresponding nodes to the open list. This operation does not traverse all the neighbors, which is the difference from the classical A* algorithm. When an expansion meets the $$y$$ node, whose neighbor is accessible, e.g., the $$z$$ node, we regard the $$y$$ node as a special one. Meanwhile, it is the destination of expansion from node $$x$$ along the straight-line direction. Then, its heuristic distance value $$h$$, namely the cost of reaching $$y$$ from $$x$$, can be formulated as follows:

(3)

$$ \begin{equation} h(y) = h(x) + D(x, y) \end{equation} $$

(4)

$$ \begin{equation} D(x, y) = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} \end{equation} $$

Figure 4. Selective strategy.

where $$(x_1, y_1)$$ and $$(x_2, y_2)$$, respectively, represent the coordinates of two nodes $$x$$ and $$y$$ and $$h(x)$$ represents the distance between child node and parent node.

3.2. Rules for improvement

In this section, we introduce some rules to reduce the number of nodes in the open list.

3.2.1. Rules of node expansion

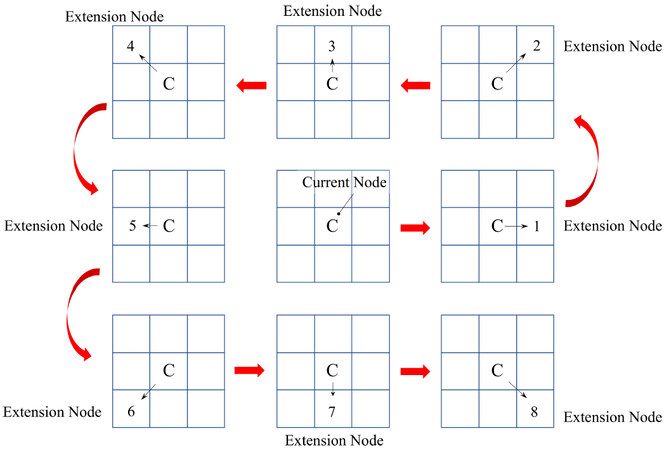
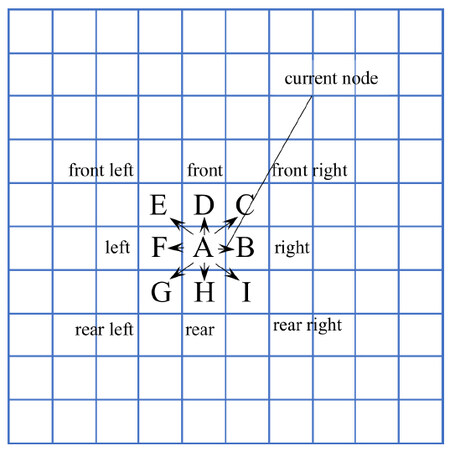
The expansion direction is shown in Figure 5. For example, the direction from $$A$$ to $$B$$ is the right one. The directions of front, rear, left, and right are collectively referred to as the straight-line direction and others are the diagonal direction. It is noted that the expansion along the diagonal direction contains the expansion in the straight one.

Figure 5. Node expansion of improved A* algorithm.

3.2.2. Rules of forced neighbor

Assume $$X$$ is the current node, $$A$$ is the neighbor node of $$X$$ in the diagonal direction, $$B$$ is the parent node of $$X$$, and $$C$$ is the non-free neighbor node. If $$A$$ meets the equation $$h(B, X)+h(X, A)<=h(B, X)+h(X, C)+h(C, A)$$, then $$A$$ is the forced neighbor. Figure 6a describes the case of equation $$h(B, X)+h(X, A)=h(B, X)+h(X, C)+h(C, A)$$. Figure 6b describes the case of equation $$h(B, X)+h(X, A)< h(B, X)+h(X, C)+h(C, A)$$

Figure 6. Force neighbors under two conditions.

3.2.3. Rules of jump points

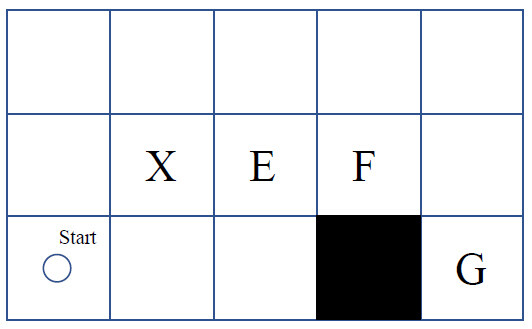
The nodes selectively chosen to expand are termed jump points. The rules are as follows. First, a node is regarded as a jump point when the node is surrounded by the forced neighbor in the diagonal direction. Second, if a node has a parent node in the diagonal direction and a reachable path in the straight direction to a jump point, then it is a jump point. Third, the starting node and the target node are stipulated as jump points. An example of finding a jump point during node expansion is shown in Figure 7.

Figure 7. Example of jump points.

It is obvious that $$F$$ node, $$G$$ node, and the start node are jump points because they satisfy the first, second, and third rules, respectively.

3.2.4. Rules of nodes

First, we demonstrate a rule of the search order. The jump points are primarily searched in the straight-line direction and then in the diagonal direction. Second, the open list only adds the jump points. The search nodes with the lowest cost are added to the closed list. The planning path is formed by the subsets of these jump points.

3.2.5. Rules of path

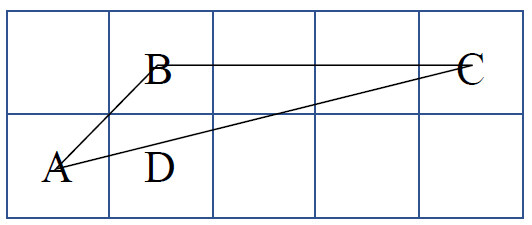
Inspired by the theorem that any side of a triangle must be shorter than the other two sides added together, a pruning method can be applied. In Figure 8, there are three consecutive nodes, i.e., $$A$$, $$B$$, and $$C$$, from the global path, and they constitute a triangle. When $$D$$ is a free grid, the path from $$A$$ to $$C$$ by $$B$$ is improved by the path from $$A$$ directly to $$C$$.

Figure 8. Rules of path.

3.3. Improved algorithm

Based on the strategy above, the improved A* algorithm is shown in Algorithm 1. The algorithm takes the grid map and initial node as inputs and outputs a feasible global path. First, the grid map is initialized and the search method of nodes is defined to expand neighbor nodes in sequence with equal probability. Then, the initial node is added to the open list (Line $$3$$). Second, it is determined whether the open list is empty or not. If it is true, the pathfinding fails. Otherwise, the pathfinding continues (Line $$5$$). Thirdly, the node with the smallest value in the open list will be moved to the closed list (Lines $$7$$–$$9$$). Then, it is discovered whether the current node is the target node or not. If it is the target, the pathfinding is successful and the solution of the path is returned (Line $$11$$). Otherwise, the jump points are found and added to the open list. Specifically, the jump points are searched along the straight direction from the parent node. When no free grid is found, the diagonal direction is considered (Lines $$13$$–$$15$$).

Algorithm 1 Improved A* algorithm.
1: input: grid_map, initial_node
2: output: global_path
3: openlist.push_back(initial_node)
4: while True do
5: if openlist.isEmpty() then return NULL
6: else
7: node $$\gets$$ FindSmallestValue(openlist)
8: openlist.erase(node)
9: closelist.push_back(node)
10: end if
11: if isTarget(node) then return GetGlobalPath(node)
12: else
13: jump_point $$\gets$$ FindJumpPoint()
14: openlist.push_back(jump_point)
15: end if
16: end while

In summary, the differences between the traditional A* and improved A* depend on the rules of constraint. The constraint successfully provides traditional A* various ways of node expansion and reduces the time of planning in the pathfinding process. Besides, the occupancy rate drops due to the decreasing nodes in the open list. In the end, the path length is trimmed because the polyline is replaced by the straight line at the inflection point of the path.

4. EXPERIMENT

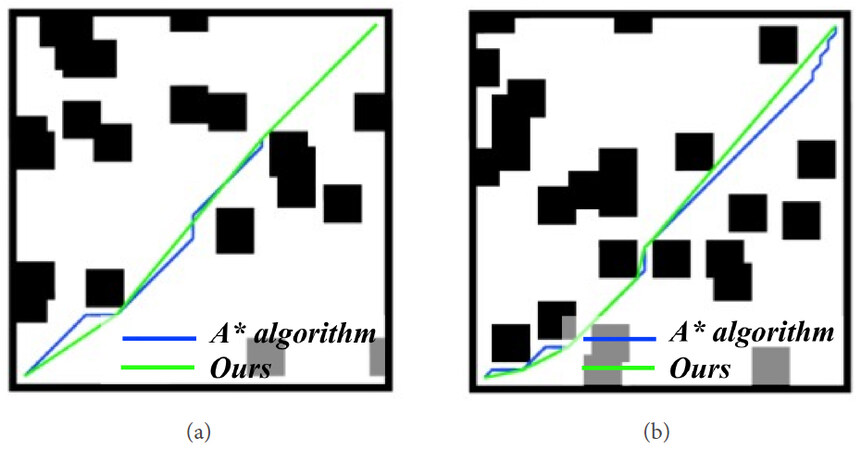
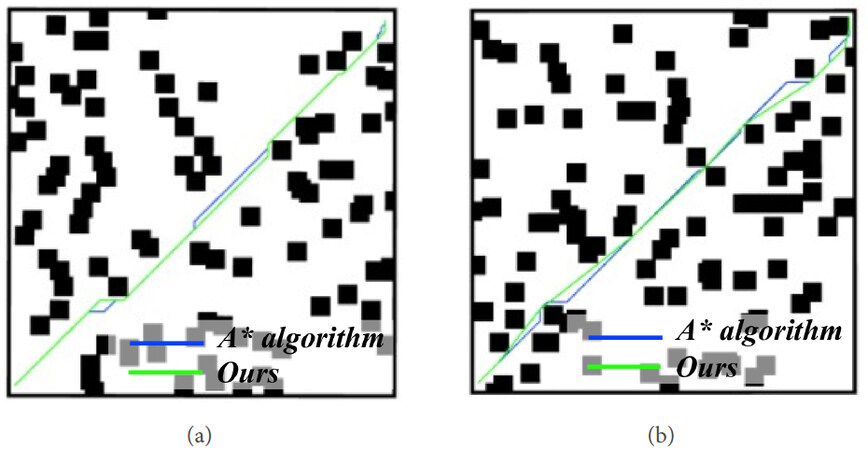
To prove the effectiveness of the improved A* algorithm, simulation experiments in C++ were carried out. At first, four grid maps with obstacles were constructed, and a simulation of the traditional A* algorithm was designed and performed. In detail, 1% of grid points were randomly regarded as the center points of the obstacle and the size of the obstacle was $$5 \times 5$$.

We noticed that many expansion nodes were stored in the open list, causing a high occupancy rate and consuming too many memory resources. Moreover, the feasible planning path was relatively optimal and the inflection point of the path could be pruned.

The grid map required for the experiment is shown in Figure 9, where the sizes of the grid maps are, respectively, $$50 \times 50$$ and $$100 \times 100$$ and the resolution is $$ 0.5 $$ m per pixel. The black grid represents the occupancy of the grid which is inaccessible. We set the starting point of the navigation task at the bottom left of the grid map and the target at the upper right.

Figure 9. Randomly generated grid maps of different size.

The simulation on $$ 50\; \times\; 50 $$ grid maps is shown in Figure 10, where the blue polyline represents the path planned by the traditional A* algorithm. The green one represents the path planned by our method. The simulation on $$ 100\; \times\; 100 $$ grid maps is shown in Figure 11,

Figure 10. Path planning on $$ 50\; \times\; 50 $$ grid maps.

Figure 11. Path planning on $$ 100\; \times\; 100 $$ grid maps.

The experimental data are shown in Tables 1 and 2. The occupancy rate is the ratio of the number of open-list nodes to the number of nodes on the grid map. In Table 1, based on the $$ 50\; \times\; 50 $$ map, the number of generated open-list nodes is $$372$$ and the occupancy rate is $$14.88%$$ before improvement. Through the improved algorithm, the number of nodes is decreased to $$89$$ and the rate is $$3.56%$$. In addition, the planning path is shortened from $$3.41$$ to $$3.31$$.

Table 1

Average Performance results on randomized $$ 50\; \times\; 50 $$ maps

	A*	Improved A*
Node numbers of open list	$$372$$	$$89$$
Occupancy rate of open list	$$14.88$$	$$3.56$$
Path length without pruning	$$3.41$$	-
Path length with pruning	-	$$3.31$$

Table 2

Average performance results on randomized $$ 100\; \times\; 100 $$ maps

	A*	Improved A*
Node numbers of open list	$$1508$$	$$272$$
Occupancy rate of open list	$$15.08$$	$$2.72$$
Path length without pruning	$$7.01$$	-
Path length with pruning	-	$$6.83$$

In Table 2, based on the $$ 100\; \times\; 100 $$ map, the count of generated open list nodes is $$1508$$ and the occupancy rate is $$15.08%$$ before improvement. By the improved algorithm, the number of nodes is decreased to $$272$$ and the rate is $$2.72%$$. In addition, the planning path is shortened from $$7.01$$ to $$6.83$$.

Comprehensive experimental results show that the improved A* algorithm can improve the node occupancy rate and shorten the path length. In other words, it provides the traditional A* method with the capabilities of higher efficiency and lower consumption of memory.

5. CONCLUSION

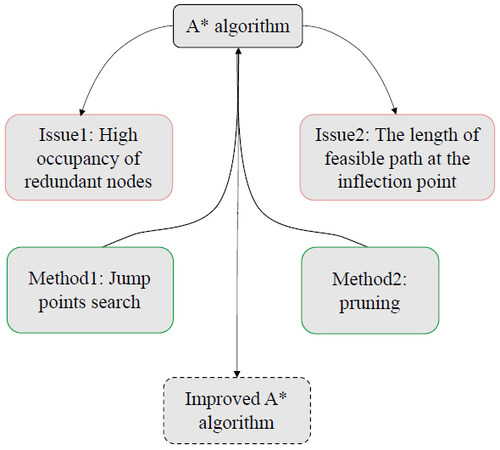
Although the solution of the traditional A* algorithm is relatively optimal, it can be further improved in two aspects. On the one hand, too much memory resource is consumed by the large number of nodes stored in the open list. On the other hand, at the inflection point of the planning path, there is a possibility to prune based on the free grid. Thus, this article proposes the following methods, as shown in Figure 12:

Figure 12. Conclusion.

1. Incorporate jump point search methods to selectively add specific properties of nodes to the open list and reduce the number of nodes.

2. Merge the pruning idea with the classical A* algorithm. A straight path is used to replace the polyline path, and the length of the path is shortened.

The simulation experiments verified the practical effect of our improved A* algorithm. In the future, we will study how to reduce the time of node traversal to improve the real-time performance of path planning.

DECLARATIONS

Authors' contributions

Writing-original draft and conceptualization: Huang H

Validation and supervision: Li Y

Investigation: Bai Q

Availability of data and materials

Not applicable.

Financial support and sponsorship

None.

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Lapierre L, Zapata R, Lepinay P. Combined path-following and obstacle avoidance control of a wheeled robot. Int J Rob Res 2007;26:361-75.

2. Diveev A, Konstantinov S. Study of the practical convergence of evolutionary algorithms for the optimal program control of a wheeled robot. J Comput Syst Sci Int 2018;57:561-80.

3. Kashyap AK, Pandey A. Different nature-inspired techniques applied for motion planning of wheeled robot: a critical review. Int J Adv Robot Autom 2018;3:1-10.

4. Li Y. Business plan for autonomous delivery robot. ICA 2020;11:33.

5. Bontikous S, Guérin A, Postaire M, et al. A drug storage delivery robot in a cold room: a new feature to consider. J Pharm Clin 2019;38:24-26.

6. Luo RC, Lin TY, Su KL. Multisensor based security robot system for intelligent building. Robotics and Autonomous Systems 2009;57:330-38.

7. Dong F, Fang S, Xu Y. Design and implementation of security robot for public safety. In: 2018 International Conference on Virtual Reality and Intelligent Systems (ICVRIS). IEEE; 2018. pp. 446-49.

8. Belanche D, Casaló LV, Flavián C, Schepers J. Service robot implementation: a theoretical framework and research agenda. The Service Industries Journal 2020;40:203-25.

9. Baraka K, Veloso MM. Mobile service robot state revealing through expressive lights: formalism, design, and evaluation. Int J of Soc Robotics 2018;10:65-92.

10. Patle B, Pandey A, Parhi D, et al. A review: on path planning strategies for navigation of mobile robot. Defence Technology 2019;15:582-606.

11. Zhang Hy, Lin Wm, Chen Ax. Path planning for the mobile robot: A review. Symmetry 2018;10:450.

12. Ghosh S, Panigrahi PK, Parhi DR. Analysis of FPA and BA meta-heuristic controllers for optimal path planning of mobile robot in cluttered environment. IET Science, Measurement & Technology 2017;11:817-28.

13. Zhang L, Li Y. Mobile robot path planning algorithm based on improved A star. In: Journal of Physics: Conference Series. vol. 1848. IOP Publishing; 2021. p. 012013.

14. Kuswadi S, Santoso JW, Tamara MN, Nuh M. Application SLAM and path planning using A-star algorithm for mobile robot in indoor disaster area. In: 2018 International Electronics Symposium on Engineering Technology and Applications (IES-ETA). IEEE; 2018. pp. 270-74.

15. Likhachev M, Koenig S. A generalized framework for lifelong planning A* search. In: ICAPS; 2005. pp. 99-108.

16. Ogata K. A generic approach on how to formally specify and model check path finding algorithms: dijkstra, A* and LPA*. Int J Soft Eng Knowl Eng 2020;30:1481-523.

17. Likhachev M, Gordon GJ, Thrun S. ARA: formal analysis 2003. Available from: http://www.cs.cmu.edu/afs/cs/Web/People/maxim/files/ara_tr.pdf.

18. Likhachev M, Gordon GJ, Thrun S. ARA*: anytime A* with provable bounds on sub-optimality. Available from: https://www.ri.cmu.edu/publications/ara-anytime-a-with-provable-bounds-on-sub-optimality/.

19. Karaman S, Walter MR, Perez A, Frazzoli E, Teller S. Anytime motion planning using the RRT. In: 2011 IEEE International Conference on Robotics and Automation. IEEE; 2011. pp. 1478-83.

20. Agarwal S, Gaurav AK, Nirala MK, Sinha S. Potential and sampling based rrt star for real-time dynamic motion planning accounting for momentum in cost function. In: International Conference on Neural Information Processing. Springer; 2018. pp. 209-21.

21. Park JK, Chung TM. Boundary-RRT* algorithm for drone collision avoidance and interleaved path re-planning. J Infn Pro Syst 2020;16:1324-42.

22. Zhang D, Xu Y, Yao X. An Improved path planning algorithm for unmanned aerial vehicle based on rrt-connect. In: 2018 37th Chinese Control Conference (CCC). IEEE; 2018. pp. 4854-58.

23. Li S, Zhao D, Sun Y, Yang J, Wang S. Path planning algorithm based on the improved RRT-connect for home service robot arms. In: 2021 IEEE International Conference on Intelligence and Safety for Robotics (ISR). IEEE; 2021. pp. 403-7.

24. Song B, Wang Z, Zou L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Applied Soft Computing 2021;100:106960.

25. Lamini C, Benhlima S, Elbekri A. Genetic algorithm based approach for autonomous mobile robot path planning. Procedia Computer Science 2018;127:180-89.

26. Konatowski S, Pawlowski P. Application of the ACO algorithm for UAV path planning. Przeglad Elektrotechniczny 2019;95:115-18.

27. Wang H, Qi X, Lou S, et al. An efficient and robust improved A* algorithm for path planning. Symmetry 2021;13:2213.

28. Song Z, Yuan L. Application of improved A algorithm in mobile robot path planning. In: 2019 3rd International Symposium on Autonomous Systems (ISAS); 2019. pp. 534-37.

29. Zhang H, Wang Y, Zheng J, Yu J. Path planning of industrial robot based on improved RRT algorithm in complex environments. IEEE Access 2018;6:53296-306.

30. Harabor D, Grastien A. Improving jump point search. In: Proceedings of the International Conference on Automated Planning and Scheduling. vol. 24; 2014. pp. 128-35. Available from: https://www.semanticscholar.org/paper/Improving-Jump-Point-Search-HaraborGrastien/f4b9b6355077685a033d38dd2392684a10fa4db6.

31. Zheng X, Tu X, Yang Q. Improved JPS algorithm using new jump point for path planning of mobile robot. In: 2019 IEEE International Conference on Mechatronics and Automation (ICMA). IEEE; 2019. pp. 2463-68.

32. Webb J. A straight line is the shortest distance between two points. The Mathematical Gazette 1974;58:137-38.

33. Wang KHC, Botea A. Tractable multi-agent path planning on grid Maps. In: IJCAI. vol. 9. Pasadena, California; 2009. pp. 1870-75. Available from: https://www.ijcai.org/Proceedings/09/Papers/310.pdf.

Cite This Article

Export citation file: BibTeX | RIS

OAE Style

Huang H, Li Y, Bai Q. An improved A star algorithm for wheeled robots path planning with jump points search and pruning method. Complex Eng Syst 2022;2:11. http://dx.doi.org/10.20517/ces.2022.12

AMA Style

Huang H, Li Y, Bai Q. An improved A star algorithm for wheeled robots path planning with jump points search and pruning method. Complex Engineering Systems. 2022; 2(3): 11. http://dx.doi.org/10.20517/ces.2022.12

Chicago/Turabian Style

Huang, Hongqian, Yanzhou Li, Qing Bai. 2022. "An improved A star algorithm for wheeled robots path planning with jump points search and pruning method" Complex Engineering Systems. 2, no.3: 11. http://dx.doi.org/10.20517/ces.2022.12

ACS Style

Huang, H.; Li Y.; Bai Q. An improved A star algorithm for wheeled robots path planning with jump points search and pruning method. Complex. Eng. Syst. 2022, 2, 11. http://dx.doi.org/10.20517/ces.2022.12

About This Article

Copyright

© The Author(s) 2022. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

1415

Downloads

644

Citations

Comments

Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.

⁰

Download PDF

Download XML 0 downloads

Cite This Article 14 clicks

Export Citation 45 clicks

Like This Article 43 likes

Share This Article

https://www.oaepublish.com/articles/ces.2022.12

Scan the QR code for reading!

See Updates

Contents

Figures

An improved A star algorithm for wheeled robots path planning with jump points search and pruning method

Hongqian Huang

Qing Bai

Abstract

Keywords

1. INTRODUCTION

2. TRADITIONAL A* ALGORITHM

2.1. Grid map

2.2. A* algorithm

3. IMPROVED A* ALGORITHM

3.1. Selective strategy

3.2. Rules for improvement

3.2.1. Rules of node expansion

3.2.2. Rules of forced neighbor

3.2.3. Rules of jump points

3.2.4. Rules of nodes

3.2.5. Rules of path

3.3. Improved algorithm

4. EXPERIMENT

5. CONCLUSION

DECLARATIONS

Authors' contributions

Availability of data and materials

Financial support and sponsorship

Conflicts of interest

Ethical approval and consent to participate

Consent for publication

Copyright

REFERENCES

Cite This Article

About This Article

Copyright

Data & Comments

Data

Comments

See Updates

Committee on Publication Ethics

Portico

Committee on Publication Ethics

Portico