Research Article | Open Access | 26 Sep 2022

A distributed electricity energy trading strategy under energy shortage environment

Views: 1133 | Downloads: 522 | Cited:

Qian Xu¹

, ...

Hongzhe Liu²

Complex Eng Syst 2022;2:14.

10.20517/ces.2022.20 | © The Author(s) 2022.

Author Information

Article Notes

Cite This Article

Abstract

This paper presents a power dispatch strategy combining the main grid and distributed generators based on aggregative game theory and the Cournot price mechanism. Such a dispatch strategy aims to increase the electricity under the power shortage situation. Under the proposed strategy, this paper designs a discrete-time algorithm fusing the estimation technique and the Digging method to solve the power shortage problem in a distributed way. The distributed algorithm can provide privacy protection and information safety and improve the power grid's extendibility. Moreover, the simulation results show that the proposed algorithm has favorable performance and effectiveness in the numerical example.

Keywords

Aggregative game, power dispatch, Cournot price mechanism, distributed discrete-time algorithm

Download PDF 0 34

1. INTRODUCTION

With the fast development of the electricity network, power networks must face a more complicated situation. Additionally, the rapidly increasing scale of the electricity networks makes the traditional centralized algorithm unable to fit the actual power dispatch process ^[1–4]. Under such a background, designing an algorithm in a distributed manner becomes a recommendable choice to meet the actual needs. In a power shortage scenario, the priority in the power grid operation lies in increasing the power supply immediately. Otherwise, the best choice is to cut the loads. However, in the actual situation, increasing the power supply is usually not an easy task when the main power source cannot offer enough power. Due to the rapid emergence of distributed generators and energy, a natural idea arises, i.e., encouraging distributed generators to turn up their outputs when a power shortage occurs. Since the distributed generators may belong to different companies or individuals, designing a reasonable strategy for increasing electricity becomes challenging. As one of the most influential and general methods, the price incentive fits the market laws and meets the practical demand. The logic behind it is quite clear, i.e., improving the power selling price for the operators when the power shortage happens. Such a strategy prompts the users to produce more energy. The strategy mentioned above involves several research fields, which are introduced in the following subsection.

1.1. Literature review

In general, the main states of the power operation can be divided into three situations: the regular running state, the power shortage state, and the collapse state. In different operation states of the power grid, distributed algorithms have different applications. Under the regular running state of the large-scale power grid, the main target focuses on a distributed economic dispatch. In this research area, there already exist fruitful results. In the early research, the distributed algorithm is used to solve the conventional economic dispatch problem only subjecting to the supply–demand global constraint. For example, Yu et al.^[5] employed the Laplacian dynamics to ensure that the incremental cost reaches a consensus. Compared with algorithm designs based on dual theory (see ^[4]), such a method avoids the update of the Lagrange multipliers and reduces the computation complexity. However, the introduction of the Lagrange multipliers endows the algorithm with the capacity to deal with the global inequality constraints (see ^[4]). On the basis of the work in ^[5], Li et al.^[6] introduced the event-triggered scheme to reduce the communication burden caused by the continuous-time algorithm. From then on, researchers began employing many methods to improve the performance and adaptation of the applicable consensus algorithm. For instance, Wen et al.^[7] presented the adaptive consensus-based robust strategy to fit the uncertain communication graph scenario. To increase the convergence of the algorithm in ^[6], He et al.^[8] designed the second-order algorithm. After that, He et al.^[9] developed an ADMM algorithm to solve the economic dispatch problem under the discrete-time communication environment. It needs to be emphasized that the above studies only focused on the dispatch problem with few fundamental constraints. To meet the requirements of the actual system, more constraints need to be considered in this given framework. These constraints include ramp-rate constraints, transmission line limit constraints, power loss constraints, etc. (see ^[4]). In recent years, since game theory is a recommendable method to describe the influence of human factors in the power dispatch models, researchers have begun to consider game theory, which extends the scope of model description. From the distributed control aspect, Liu et al.^[3] proposed a non-cooperative distributed coordination control strategy to address the multi-operator energy trading problem. Such a strategy involves electricity trading during the control process and makes the model more reasonable. From the game and optimization aspect, Ye et al.^[10] introduced the Cournot price mechanism to describe the market trading process. This mechanism makes the price change with the total energy demand and matches the law of the market. Based on the work in ^[10], Fu et al.^[11] introduced more constraints in the market trading process. Such an adjustment also changes the algorithm design principle and introduces the multiplier consensus algorithm to deal with the global constraints. A similar technique also can be found in ^{[12, 13]}. Besides, the authors of ^[13] also introduced some techniques applicable to the non-smooth case.

1.2. Feature of the paper

This paper aims to design a distributed strategy for electricity trading in an energy shortage environment. Such a strategy is required to match the law of the market and adapt to the complicated communication graph. Furthermore, in the process of implementing the above strategy, there also exist the following challenges:

● The enormous number of distributed generators makes it impossible for the centralized algorithm to dispatch all distributed power simultaneously to compensate for the power shortage.

● How to design a suitable strategy that ensures the benefits of all the generators and maintains the initiative of the power operator (i.e., the pricing power) is the main difficulty in trading strategy design.

● Due to the character of the complicated communication graph, employing a discrete-time algorithm design principle becomes the first choice ^[4].

To solve the above challenges, this paper first formulates the power shortage situation as an aggregative game involving the Cournot price mechanism. In this game, the electricity is supplied by two parts: one is the main power grid, and the other consists of distributed generators. Then, this paper designs a distributed strategy based on the Digging algorithm ^[14] and the estimation strategy ^[15]. The features of this distributed strategy are concluded as follows:

● The discrete-time algorithm construct offers the power grid dispatch process favorable properties of privacy protection, information safety, and extendibility.

● The employment of the Cournot price mechanism aggregates the distributed generators within a feasible and market-determined framework.

The rest of the paper is arranged as follows. The problem formulation is introduced in the next section. Then, the problem analysis section is presented to analyze the proposed problem and explain the designed algorithm. The simulation results are given to verify the proposed algorithm's performance and effectiveness in the simulation section. The last section concludes the paper.

2. PROBLEM FORMULATION

In this section, we introduce an aggregative game model to describe the electricity energy trading. By solving this game, we aim to design a distributed strategy that encourages operators to supply electricity to the main grid. When the power on the main grid is insufficient (caused by attacks, generator failures, or capacity limitations), such a strategy allows us to adjust the sold price of electricity. After promoting the sold price of electricity, the operators will benefit more by selling more electricity, which improves the motivations of the operators and conforms to the law of the market. The detailed model is presented as:

(1)

$$ \begin{align} \begin{matrix} \min\limits_{i\in \mathcal{N}}& C_i\left( P_i, G_i \right) -R_i\left(P_1, \cdots, P_N \right)\\ \mathrm{s}.\mathrm{t}.& \sum\limits_{i=1}^N{P_i}+\sum\limits_{i=1}^N{G_i}=\sum\limits_{i=1}^N{D_i}, \\ & P_{i}^{\min}\le P_i\le P_{i}^{\max}, \\ & G_{i}^{\min}\le G_i\le G_{i}^{\max}, \\ \end{matrix} \end{align} $$

where $$ P_i $$ and $$ G_i $$ denote the power output of the distributed generators and the power obtained from the main grid in the operator $$ i $$ node, respectively, which comply with the output limits presented as the second and the third constraints of the problem in Equation (1) with the superscripts $$ \min $$ and $$ \max $$ denoting the minimal and maximal values of the corresponding variables. $$ D_i $$ represents the load demand in operator $$ i $$ node and $$ \mathcal{N}=\{1, \dots, N\} $$ represents the operator index set. The power balance limit is described as the first constraint of the problem in Equation (1). The cost function of each operator $$ i $$ is defined as follows:

$$ C_i\left( P_i, G_i \right) =a_iP_{i}^{2}+b_iP_i+c_i+\alpha _iG_{i}^{2}+\beta _iG_i+\gamma _i, $$

where $$ a_i $$, $$ b_i $$, $$ c_i $$, $$ \alpha_i $$, $$ \beta_i $$, and $$ \gamma_i $$ are positive parameters, $$ C_i\left( P_i, G_i \right) $$ represents the electricity cost of the operator $$ i $$, the additional value added for the operator $$ i $$ is described as

$$ R_i\left( P_1, \cdots , P_N \right) =\left( -r\sum\limits_{i=1}^N{P_i}+l \right) P_i, $$

where $$ r $$ and $$ l $$ are both positive parameters adjusted by the main grid. Note that the additional value added function is designed based on the Cournot price model, and it can be considered as an extra bonus for the power supply provided by the operators. When the total power of the distributed generators increases, the additional value added will decrease. When the main grid turns up the parameters $$ r $$ and $$ l $$, the additional value added will go up, which contributes to the increase of the distributed generators output. Figure 1 concludes the above process and the challenges.

A distributed electricity energy trading strategy under energy shortage environment

Figure 1. Explanation for the problem in Equation (1)

Compared with the optimization problem, the problem in Equation (1) has multiple objection functions. Such a problem setting makes the aggregative game in Equation (1) possess the capacity to consider each operator's cost independently rather than the sum of the cost.

3. PROBLEM ANALYSIS

In this section, we analyze the proposed problem in Equation (1) based on Lagrange dual theory and game theory. Note that the problem in Equation (1) is a game theory problem, thus some transformations are required such that it can match the framework of the distributed algorithm. For convenience, define the local objective function $$ F_i\left( P_i, G_i \right) $$ of the problem in Equation (1) as follows:

(2)

$$ F_i\left( P, G_i \right) =C_i\left( P_i, G_i \right) -R_i\left( P_1, \cdots , P_N \right). $$

Note that $$ P_i $$ and $$ G_i $$ are the decision variables of the operator $$ i $$ in the above definition (Equation (2)), while other operators' decisions are considered as independent variables. Define the pseudo-gradient $$ \nabla F\left( S \right) $$ as

(3)

$$ \begin{align} \nabla F\left( S \right) \triangleq \left[ \begin{matrix} \nabla F_1\left( P_1, G_1 \right)\\ \vdots\\ \nabla F_N\left( P_N, G_N \right)\\ \end{matrix} \right], \end{align} $$

where $$ S=\left[ P_1, G_1\dots , P_N, G_N \right] ^T $$. To keep the later analysis going on wheel, we assume that the problem in Equation (1) satisfies the following assumption:

Assumption 1The pseudo-gradient $$ \nabla F\left( S \right) $$ consisting of the gradients of the local objective functions satisfies the following monotone condition,

(4)

$$ \left< \nabla F\left( S \right) -\nabla F \, ( \bar{S} ) , S-\bar{S} \right> \ge \frac{\sigma}{2} \Vert S-\bar{S} \Vert _{2}^{2}, \ \ \ \ \forall \bar{S}\in \Omega , $$

where $$ \sigma >0 $$ is the strongly monotone parameter and $$ \Omega $$ represents the feasible set restricted by all the constraints in Equation (1).

Based on the Lagrange dual theory, we can define the Lagrange dual function as follows:

(5)

$$ d_i(\lambda_i) = \min\limits_{\left( P_i, G_i \right)\in \Omega _i} \left\{ F_i\left( P, G_i \right) +\left< \lambda _i, \sum\limits_{i=1}^N{P_i}+\sum\limits_{i=1}^N{G_i}-\sum\limits_{i=1}^N{D_i} \right>\right\}, $$

where $$ \lambda_i $$ denotes the Lagrange multipliers of the operator $$ i\in \mathcal{N} $$, $$ d_i(\lambda_i) $$ is the function only associated with $$ \lambda_i $$, and $$ \Omega_i $$ represents the feasible local set defined as

$$ \Omega _i=\left\{ \left( P_i, G_i \right)\in \mathbb{R}^2\mid P_{i}^{\min}\le P_i\le P_{i}^{\max}, G_{i}^{\min}\le G_i\le G_{i}^{\max} \right\}. $$

Note that the rivals' decisions $$ P_1, \dots, P_{i-1}, P_{i+1}, \dots, P_N $$ are considered as the exogenous variables. Since the feasible set of the problem in Equation (1) is a hyperplane, we can obtain the optimal solution of Equation (1) by solving the following dual problem:

(6)

$$ \forall i \in \mathcal{N}, \ \ \ \max\limits_{\lambda_i} \ \ \ d_i(\lambda_i). $$

Clearly, problem in Equation (6) is still a game problem that has no constraints. To transform the above problem in Equation (6) into a problem suitable for the distributed algorithm framework, some stronger restrictions are required. According to the analysis in ^[16] (Theorem 1), the variational solution is the generalized Nash equilibrium ^[17] of Equation (6). For such a solution, all the associated optimal Lagrange multipliers $$ \lambda_i $$ with $$ i\in\mathcal{N} $$ have the same value. By considering this as a constraint in the above problem (Equation (6)), we can obtain the following problem:

(7)

$$ \max\limits_{\lambda} \ \ \ -\sum\limits_{i=1}^N{F_i^*\left( \lambda _i \right)} \ \ \ \mathrm{s}.\mathrm{t} \ \ \ \lambda _i=\cdots =\lambda _N, $$

where $$ \lambda =[ \lambda _{1}, \dots , \lambda _{N} ] ^T $$, and the conjugate function $$ F_i^*\left( \lambda _i \right) $$ is defined as

(8)

$$ F_i^*\left( \lambda _i \right) \triangleq \max\limits_{\left( P_i, G_i \right) \in \Omega _i} \left\{ -F_i\left( P, G_i \right) -\left< \lambda _i, P_i+G_i-D_i \right> \right\}. $$

We need to emphasize that the variational solution of a game problem is only one of the generalized Nash equilibria. In other words, we cannot obtain all the generalized Nash equilibria by solving different variational inequalities ^[17]. Based on Theorem 12.60 stated in ^[18], the conjugate function $$ F_i^*\left( \lambda _i \right) $$ is a strong convex function with respect to $$ \lambda_i $$, $$ i\in\mathcal{N} $$. Clearly, the problem in Equation (7) is no longer a game problem but an optimization problem. Besides, the objection function of the problem in Equation (7) has no variable coupling. According to the analysis in ^[19] (Section 1.5), the constraint in Equation (7) can be replaced by the constraint $$ \left( I+W \right) \lambda=0 $$, where $$ I $$ and $$ W $$ represent the identity matrix and the nonnegative double stochastic matrix, respectively. Then, on the basis of the dual theory and the augmented Lagrange method ^[20], we can transform the problem in Equation (7) into the following unconstrained optimization problem:

(9)

$$ \max\limits_{\theta}\, \, \, \min\limits_{\lambda} \Bigg\{ \sum\limits_{i=1}^N{F_i^*\left( \lambda _i \right)}+\left< \lambda , \left( I+W \right) \lambda \right> +\left< \theta , \left( I+W \right) \lambda \right> \Bigg\}, $$

where $$ \left< \lambda , \left( I+W \right) \lambda \right> $$ represents the augmented item and $$ \theta $$ denotes the Lagrange multiplier with respect to the consensus constraint of the problem in Equation (7). To solve the dual problem presented above, a distributed algorithm is proposed in this paper:

(10)

$$ (P_i\left( k+1 \right), G_i\left( k+1 \right)) \ =\mathop {\mathrm{arg}\min} \limits_{\left( P_i, G_i \right)\in \Omega _i}\big\{ \bar{F}_i\left( P_i, P_i\left( k \right), G_i, u_i\left( k \right) \right)+\left< \lambda _i\left( k \right), P_i+G_i-D_i \right> \big\}, $$

(11)

$$ \lambda _i\left( k+1 \right) \ =\sum\limits_{j=1}^N{W_{ij}\left( k \right)\lambda _i\left( k \right)}-\delta y_i\left( k \right), $$

(12)

$$ y_i\left( k+1 \right) \ =\sum\limits_{j=1}^N{W_{ij}\left( k \right)y_i\left( k \right)} +\left( P_i\left( k \right) -P_i\left( k+1 \right) \right)+\left( G_i\left( k \right) -G_i\left( k+1 \right) \right), $$

(13)

$$ u_i\left( k+1 \right) \ =\sum\limits_{j=1}^N{W_{ij}\left( k \right) u_i\left( k \right)}+P_i\left( k+1 \right) -P_i\left( k \right), $$

where $$ \delta>0 $$ denotes the step-size of the designed algorithm, the initial value satisfies $$ y_i\left( 0 \right) =-P_i\left( 0 \right)-G_i\left( 0 \right)+D_i $$ and $$ u_i\left( 0 \right)=P_i\left( 0 \right) $$, and $$ {\mathrm{arg}\min} $$ denotes the variable which can make the corresponding function achieve its minimum value. We use the subscripts $$ i $$ and $$ j $$ to represent the $$ i $$th row and $$ j $$th column of matrix $$ W(k) $$. Moreover, $$ W(k) $$ satisfies Assumptions 3.1–3.3 in ^[14]. The function $$ \bar{F}_i\left( P_i, P_i\left( k \right), G_i, u_i\left( k \right) \right) $$ is defined as

(14)

$$ \bar{F}_i\left( P_i, P_i\left( k \right), G_i, u_i\left( k \right) \right) =C_i\left( P_i, G_i \right) -\left( -rNu_i\left( k \right) +l+rP_i\left( k \right) \right) P_i +rP_i^2 . $$

By following the analysis in ^[14] (Lemma 3.13), we can confirm that if the initial condition satisfies $$ y_i\left( 0 \right) =-P_i\left( 0 \right)-G_i\left( 0 \right)+D_i $$ and the sum of all $$ y_i \left( k \right) $$ is always equal to the gradient of $$ \bar{F}_i\left( P_i\left( k \right), P_i\left( k \right) , G_i\left( k \right), u_i\left( k \right) \right) $$ for all $$ k\ge 0 $$. In other words, $$ y_i \left( k \right) $$ is used to track the corresponding local gradient. Similarly, $$ u_i\left( k \right) $$ is employed to track the sum of all $$ P_i \left( k \right) $$. If the algorithm converges, $$ \lambda_i \left( k+1 \right) $$ and $$ u_i \left( k+1 \right) $$ will reach the average consensus when $$ k\to \infty $$, i.e.,

(15)

$$ \lambda_1 \left( k+1 \right)=\cdots=\lambda_N \left( k+1 \right), \, \, \, \, \, u_1 \left( k+1 \right)=\cdots=u_N \left( k+1 \right)=\frac{1}{N}\sum\limits_{i=1}^N{P_i \left( k+1 \right)}. $$

The above result also implies $$ y_1 \left( k+1 \right)=\cdots=y_N \left( k+1 \right)=0 $$. Hence, by a simple verification and the KKT condition of Equation (1) (refer to ^[17]), we can deduce that, if the algorithm converges, it converges to the solution of Equation (1).

Obviously, the optimal sub-problem within the proposed algorithm is a simple quadratic programming problem with the box constraints, which can be solved by a simple method at every iteration. Note that the algorithm proposed above is a fully distributed algorithm and the time-varying stochastic matrix allows the communication links among the agents to varying from different iterations. Compared to the decaying step-sizes, the constant step-size $$ \delta $$ employed here helps improve the proposed algorithm's convergence rate.

Remark 1The proposed algorithm is designed based on the combination of the Digging algorithm proposed in ^[14] and the distributed algorithm presented in ^[15]. In this paper, the Digging algorithm is used to calculate the optimal strategy of each operator, while the distributed estimation of the total power of the distributed generators is updated in a distributed way, which has a similar construct to the algorithm proposed in the reference ^[14]. Hence, to confirm the convergence result of the algorithm proposed in this paper, the combination of the analysis methods in ^{[14, 15]} is an effective method. First, the small gain theory introduced in ^[14] is employed to construct the convergence structure cyclic of the algorithm proposed in this paper. Second, the analysis methods used in ^[15] is used to quantify the influences caused by the aggregative variables.

4. SIMULATION

In this section, a simulation based on IEEE 14 bus is presented to verify the performance of the proposed algorithm. Table 1 shows the main grid generator cost coefficients of the proposed case. The coefficients, which include cost coefficients, constraints, and initial power, are presented in Table 2. The load demand of each operator is selected as $$ D=[ 205, 60, 30, 30, 28, 35]^T (\mathrm{p.u.}) $$, and the parameters $$ r $$ and $$ l $$ are chosen as $$ 0.00001 ( \$$ /\mathrm{p.u.^2}) $$ and $$ 0.02 ( \$$ /\mathrm{p.u.}) $$, respectively. We set the step-size as $$ \delta=0.002 $$ and assume that the communication graphs satisfy the satisfies Assumptions 3.1–3.3 in ^[14] and switch randomly.

Table 1

The main grid cost coefficients and constraints

Generator	$$ a_i\, ( \$$ /\mathrm{p.u.^2}) $$	$$ b_i \, ( \$$ /\mathrm{p.u}) $$	$$ c_i \, ( \$$ ) $$	$$ P_{i}^{\min} \, (\mathrm{p.u.}) $$	$$ P_{i}^{\max}\, (\mathrm{p.u.}) $$	Initial power$$ (\mathrm{p.u.}) $$
$$ P_1 $$	0.0037	2	1	50	200	140
$$ P_2 $$	0.0175	1.75	0.75	20	80	40
$$ P_3 $$	0.0625	1	0.75	15	50	35
$$ P_4 $$	0.0083	3	1.25	10	35	20
$$ P_5 $$	0.025	2	2	10	40	15
$$ P_6 $$	0.025	1.5	1	12	40	23

Table 2

The distributed generator cost coefficients and constraints

Generator	$$ \alpha_i\, ( \$$ /\mathrm{p.u.^2}) $$	$$ \beta_i \, ( \$$ /\mathrm{p.u}) $$	$$ \gamma_i\, ( \$$ ) $$	$$ G_{i}^{\min}\, (\mathrm{p.u.}) $$	$$ G_{i}^{\max}\, (\mathrm{p.u.}) $$	Initial power$$ (\mathrm{p.u.}) $$
$$ G_1 $$	0.064	1.25	0.75	8	70	40
$$ G_2 $$	0.0638	1.35	0.25	13	50	30
$$ G_3 $$	0.0622	1.5	0.5	8	20	18
$$ G_4 $$	0.0628	2.15	1.25	5	25	20
$$ G_5 $$	0.0653	2	1.75	7	20	14
$$ G_6 $$	0.0658	2	2	5	20	12

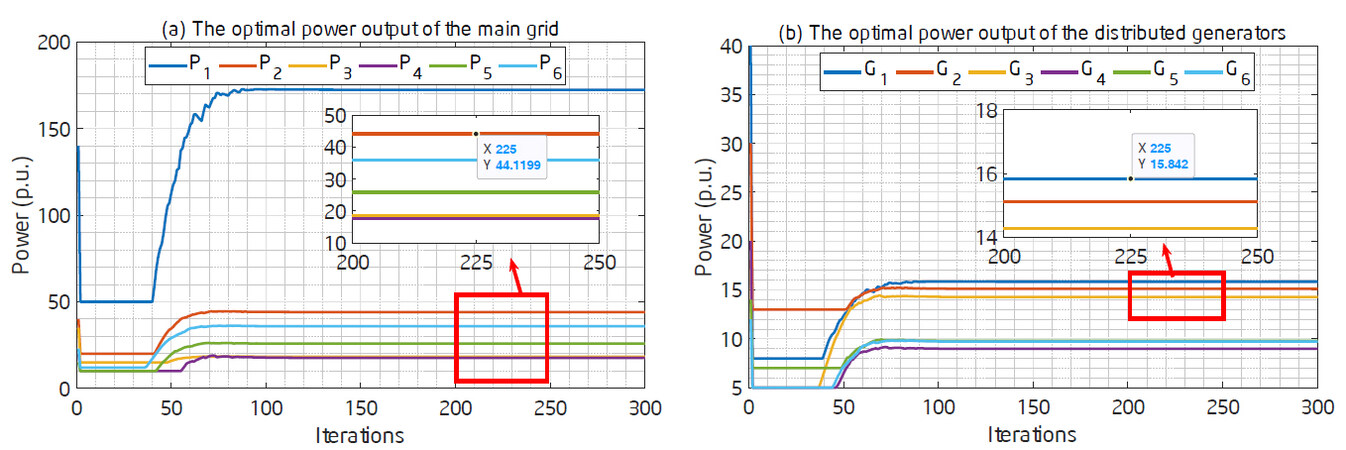
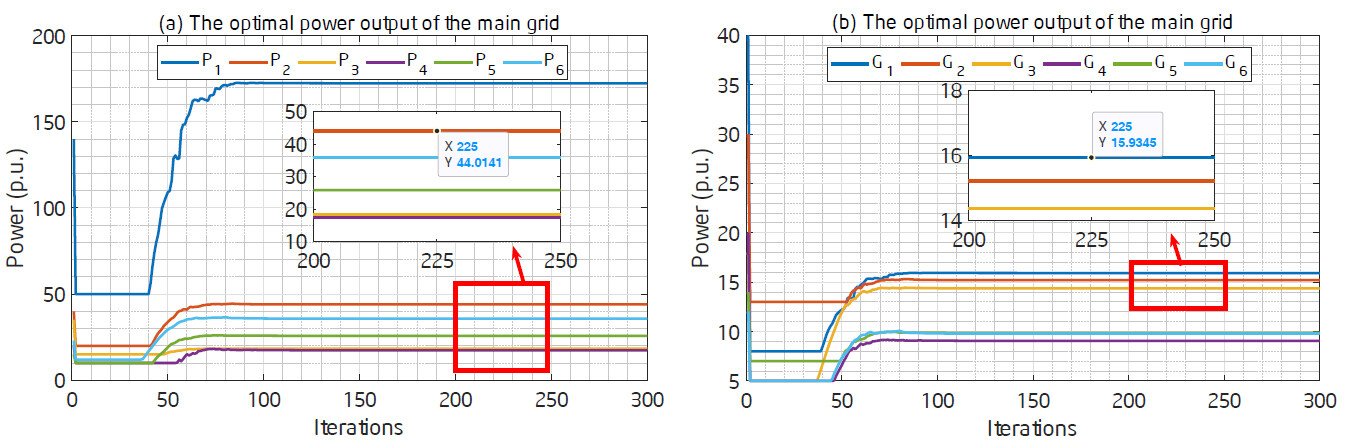
Figure 2a shows the evolutionary trajectory of the optimal power output of the main grid. As shown in Figure 2a, the power output converges to a stable state after 100 iterations, which implies that the designed algorithm has a fast convergence rate under the time-varying communication graph environment. Figure 2b shows the evolutionary track of the optimal power output of the distributed generators. Similarly, the evolutionary track converges to a stable state at around 100 iterations. Note that there exist some fluctuations during the convergence of the algorithm. These fluctuations are caused by the time variation of the communication graph and can be eliminated if the communication graph is fixed.

Figure 2. The optimal power output.

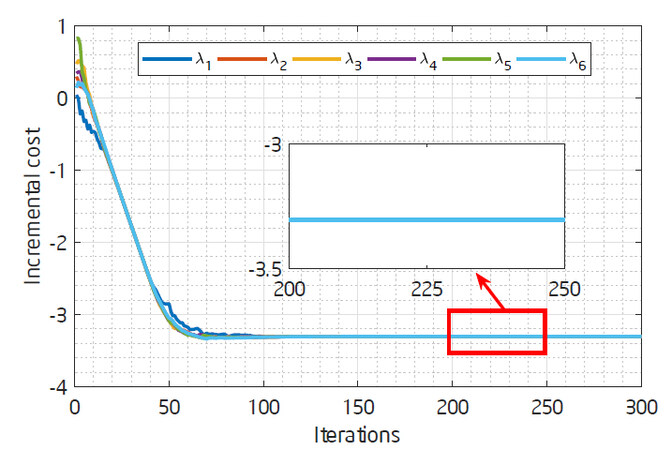
The incremental cost of each operator is shown in Figure 3. The consensus of the incremental cost (i.e., the value of $$ \lambda $$) implies that the algorithm converges to the solution satisfying the condition in Equation (15) and the equality constraint in Equation (7). As shown in Figure 4a, the estimation of the sum of all the power outputs, $$ P_i $$, $$ i\in\mathcal{N} $$, converges to a consensus value under the situation that the communication graph is time-varying. Figure 4 b confirms that the estimations obtained from each operator are consistent with the actual value, which reflects that the proposed algorithm has a favorable performance on the aggregation of the corresponding decisions. Figure 4 indicates that the proposed algorithm has a favorable convergence even if some information is based on estimation.

Figure 3. The incremental cost of each operator.

Figure 4. The estimation value and the estimation error.

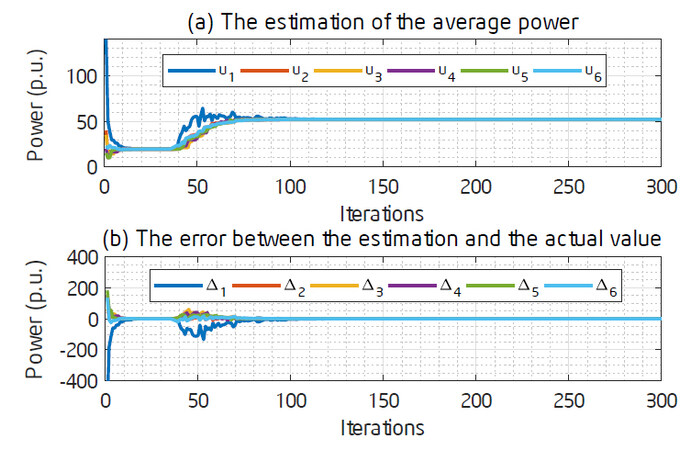
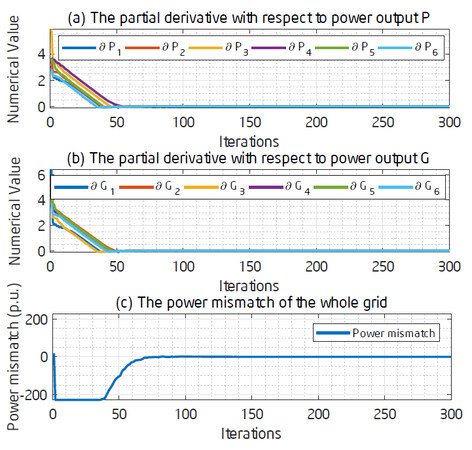
In this case, all the optimal outputs of $$ P $$ and $$ G $$ are within the given limits, which means that, if the convergence values of the proposed algorithm are the optimal solution, the partial derivative of the function $$ \bar{F}_i\left( P_i, P_i\left( k \right), G_i, u_i\left( k \right) \right) +\left< \lambda _i\left( k \right), P_i+G_i-D_i \right> $$ must be equal to $$ 0 $$. The aforementioned optimal condition is confirmed by the results in Figure 5a, b. Figure 5c shows that the mismatch of the whole power grid is equal to $$ 0 $$, which means that the proposed algorithm can maintain the global power balance constraint when the algorithm converges. Hence, by combining the results in Figures 2–5, we can verify that the algorithm converges to the KKT solution of Equation (7).

Figure 5. The partial derivative and the power mismatch.

Figure 6 shows the optimal output of the main grid and distributed generators when the Cournot price mechanism is nonexistent [i.e., deleting $$ R_i $$ in Equation (2)]. By comparing Figures 2 and 6, we can observe that the distributed generators' output decrease and the main grid's output increase when the Cournot price incentives are absent. Such results show that the Cournot price incentives can stimulate operators to increase the output when the power grid is in an energy shortage environment. Besides, setting a larger $$ l $$ and smaller $$ r $$ will help to increase the distributed generators' output.

Figure 6. The optimal power output without the Cournot price mechanism.

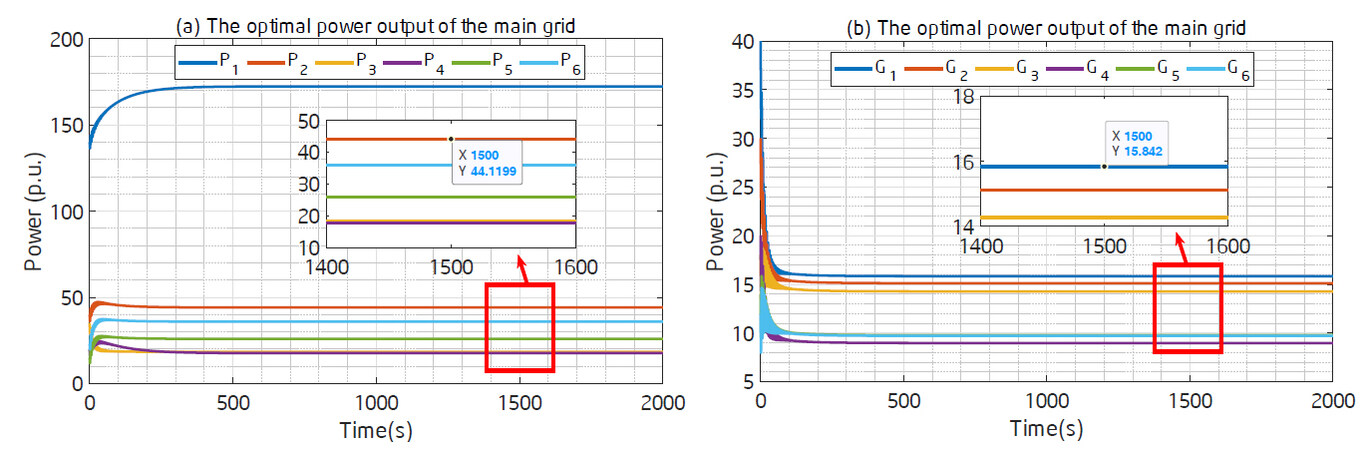
We next employ the algorithm proposed in ^[11] to make a comparison. Since the algorithm proposed in ^[11] is a continuous-time algorithm and the communication graph is fixed, we assume that the communication graph is a ring, and the abscissa is time instead of iterations. As shown in Figure 7, we can observe that the two algorithms converge to the same optimal solution. However, the algorithm proposed in ^[11] asks for a fixed communication graph and continuous-time calculation. Such a requirement may not be suitable for some wireless networks operated in a discrete time.

Figure 7. The optimal power output calculated by the continuous-time algorithm.

5. CONCLUSION

In this paper, based on an aggregative game, we design a distributed electricity energy strategy to encourage the operators to supply electricity when the power output of the main grid is in a shortage situation. The simulation results confirm the performance and effectiveness of the proposed strategy/algorithm. In future work, based on the push-sum algorithm analytical framework and the corresponding discrete algorithm, we will further analyze the convergence of the proposed strategy by a rigorous mathematical method.

DECLARATIONS

Authors' contributions

Made substantial contributions to conception and design of the study and performed data analysis and interpretation: Fu Z, Liu H

Performed data acquisition, as well as provided administrative, technical, and material support: Xu Q, Yu C, Yuan X

Availability of data and materials

Not applicable.

Financial support and sponsorship

This work was supported by the Science and Technology Project from State Grid Zhejiang Electric Power CO. Ltd (5211JY20001Q).

Conflicts of interest

All authors declared that there are no conflicts of interest.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Hu X, Liu ZW, Wen G, Yu X, Li C. Branch-wise parallel successive algorithm for online voltage regulation in distribution networks. IEEE Trans Smart Grid 2019;10:6678-89.

2. Hu X, Liu ZW, Wen G, Yu X, Liu C. Voltage control for distribution networks via coordinated regulation of active and reactive power of DGs. IEEE Trans Smart Grid 2020;11:4017-31.

3. Liu ZW, Wen G, Yu X, Guan ZH, Huang T. Delayed impulsive control for consensus of multiagent systems with switching communication graphs. IEEE Trans Cybern 2020;50:3045-55.

4. Wang K, Fu Z, Xu Q, Chen D, Wang L, Yu W. Distributed fixed step-size algorithm for dynamic economic dispatch with power flow limits. Sci China Inf Sci 2021;64 2021;64:1-13.

5. Yu W, Li C, Yu X, Wen G, Lü J. Economic power dispatch in smart grids: a framework for distributed optimization and consensus dynamics. Sci China Inf Sci 2018;61:1-16.

6. Li C, Yu X, Yu W, Huang T, Liu ZW. Distributed event-triggered scheme for economic dispatch in smart grids. IEEE Trans Ind Inf 2015;12:1775-85.

7. Wen G, Yu X, Liu ZW, Yu W. Adaptive consensus-based robust strategy for economic dispatch of smart grids subject to communication uncertainties. IEEE Trans Ind Inf 2017;14:2484-96.

8. He X, Ho DW, Huang T, Yu J, Abu-Rub H, et al. Second-order continuous-time algorithms for economic power dispatch in smart grids. IEEE Trans Syst Man Cybern, Syst 2017;48:1482-92.

9. He X, Zhao Y, Huang T. Optimizing the dynamic economic dispatch problem by the distributed consensus-based ADMM approach. IEEE Trans Ind Inf 2019;16:3210-21.

10. Ye M, Hu G. Distributed Nash equilibrium seeking in multiagent games under switching communication topologies. IEEE Trans Cybern 2017;48:3208-17.

11. Fu Z, Yu W, Lü J, Yao Y, Mei F. A distributed normalized Nash equilibrium seeking algorithm for power allocation among micro-grids. Sci China Technol Sci 2021;64:341-52.

12. Zhu Y, Yu W, Wen G, Chen G. Distributed Nash equilibrium seeking in an aggregative game on a directed graph. IEEE Trans Automat Contr 2020;66:2746-53.

13. Zhu Y, Wen G, Yu W, Yu X. Nonsmooth resource allocation of multiagent systems with disturbances: A proximal approach. IEEE Trans Control Netw Syst 2021;8:1454-64.

14. Nedic A, Olshevsky A, Shi W. Achieving geometric convergence for distributed optimization over time-varying graphs. SIAM J Optim 2017;27:2597-633.

15. Koshal J, Nedić A, Shanbhag UV. Distributed algorithms for aggregative games on graphs. Operations Research 2016;64:680-704.

16. Yi P, Pavel L. An operator splitting approach for distributed generalized Nash equilibria computation. Automatica 2019;102:111-21.

17. Nabetani K, Tseng P, Fukushima M. Parametrized variational inequality approaches to generalized Nash equilibrium problems with shared constraints. Comput Optim Appl 2011;48:423-52.

18. Rockafellar RT. Convex analysis. vol. 18. Princeton university press; 1970.

19. Chung FR, Graham FC. Spectral graph theory. vol. 92. American Mathematical Soc.; 1997.

20. Rockafellar RT. Augmented Lagrange multiplier functions and duality in nonconvex programming. SIAM J Contr 1974;12:268-85.

Cite This Article

Export citation file: BibTeX | RIS

OAE Style

Xu Q, Yu C, Yuan X, Fu Z, Liu H. A distributed electricity energy trading strategy under energy shortage environment. Complex Eng Syst 2022;2:14. http://dx.doi.org/10.20517/ces.2022.20

AMA Style

Xu Q, Yu C, Yuan X, Fu Z, Liu H. A distributed electricity energy trading strategy under energy shortage environment. Complex Engineering Systems. 2022; 2(3): 14. http://dx.doi.org/10.20517/ces.2022.20

Chicago/Turabian Style

Xu, Qian, Chutian Yu, Xiang Yuan, Zao Fu, Hongzhe Liu. 2022. "A distributed electricity energy trading strategy under energy shortage environment" Complex Engineering Systems. 2, no.3: 14. http://dx.doi.org/10.20517/ces.2022.20

ACS Style

Xu, Q.; Yu C.; Yuan X.; Fu Z.; Liu H. A distributed electricity energy trading strategy under energy shortage environment. Complex. Eng. Syst. 2022, 2, 14. http://dx.doi.org/10.20517/ces.2022.20

About This Article

Special Issue

This article belongs to the Special Issue Recent Advance on Stability, Control and Applications of Dynamical Systems

Copyright

© The Author(s) 2022. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

1133

Downloads

522

Citations

Comments

Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.