Pulsar identification based on generative adversarial network and residual network
Abstract
The search for pulsars is an important area of study in modern astronomy. The amount of collected pulsar data is increasing exponentially as the performance of modern radio telescopes improves, necessitating the improvement of the original pulsar search methods. Artificial intelligence techniques are currently being used in pulsar candidate identification tasks. However, improving the accuracy of pulsar candidate identification using artificial intelligence techniques remains a challenge. Because the amount of collected data is so large, the number of real pulsar samples is very limited, which leads to a serious sample imbalance problem. Many existing methods ignore this issue, making it difficult for the model to reach the optimal solution. A framework combining generative adversarial networks and residual networks is proposed to greatly alleviate the problem of sample inequality. The framework first generates stable pulsar images using generative adversarial networks and then designs a deep neural network model based on residual networks to identify pulsar candidates using intra-block and inter-block residual connectivity. The ResNet approach has a better ability to fit the data than the CNN approach and can achieve the extraction of features with more classification ability with a smaller dataset. Meanwhile, the data expanded by the high-quality simulated samples generated by the generative adversarial network can provide richer identification features and improve the identification accuracy for pulsar candidates.
Keywords
1. INTRODUCTION
The search for pulsars is of great importance in the study of astronomy, physics and other fields, including gravitational waves, state equations of dense substances, stellar evolution, dark matter and dark energy, and the formation and evolution of binary and multiple star systems. Therefore, the discovery of new pulsars and the exploration of their substantial scientific research potential are of great value and importance.
At present, more than 2, 700 pulsars have been discovered in the whole galaxy [1]. Most of the pulsars were discovered by modern radio telescopes, which receive periodic radio signals, pre-process them and package them into the data we need. The generation of pulsar candidates from the collected data is basically divided into three procedures which are eliminating RFI, de-dispersion, and fast fourier transform (FFT)[2]. This strategy is generally how the samples of pulsar candidates are generated. With the continuous improvement of modern radio telescopes, samples of pulsar candidates have increased, but only a small fraction of these samples are real pulsars due to the presence of RF interference and different noise sources. As a result, the real sample of pulsar candidates is much smaller than the non-real sample. In traditional studies, manual experts review each candidate in 1-300 s [3], and it takes more than 70, 000 h to examine millions of pulsar candidates. Therefore, it is crucial to investigate an automatic, efficient and accurate method for pulsar candidate identification.
In recent years, a large number of object detection methods based on neural networks have been proposed[4], many of which have been selected for pulsar candidate detection. Pulsar candidate identification methods based on neural networks have been proposed to handle the huge amount of pulsar data. Bates et al. [5] used artificial neural networks to automatically identify plausible pulsar candidates from pulsar measurements. Morello et al. [6] proposed a method called SPINN (Straightforward Pulsar Identification using Neural Networks), which designed a pulsar candidate classifier that tended to maximize the recall of identification. Zhu et al. [7] developed a pulsar image-based classification system (PICS) that used image pattern recognition and deep neural networks to identify pulsars in recent measurements, and Lyon et al. [8] proposed the decision tree-based recognition model Very Fast Decision Tree (VFDT), a method that found 20 new pulsars using the LOTAAS dataset.
Although the above neural network-based methods have achieved good identification results on the corresponding datasets and helped astronomers discover new pulsars, there are still some problems. Among the currently available pulsar candidate data, the number of positive samples (real pulsars) among the labelled pulsar candidates is extremely limited, and the number of negative samples (non-real pulsars) is much higher than the number of positive samples. In this case, when some deep learning models are directly used for training, the imbalance between the number of positive and negative samples leads to poor classification, overfitting, and even possible training failure. To address this issue, Lyon et al. [9] confirmed that the imbalance problem of pulsar candidate samples reduces the recall of pulsars by executing different classifiers on the HTRU dataset [10]. Then Lyon et al. [11] proposed using the Hellinger distance (HDT) as a splitting criterion for VFDT, thus alleviating the sample imbalance problem. In addition, GAN methods have recently been widely used in pulsar candidate identification [12]. For example, Guo et al. [13] proposed using Generative Adversarial Networks (GAN) [14] to generate some positive pulsar sample data to alleviate the problem of low recall for pulsar candidate identification models on unbalanced datasets.
Although the above methods can alleviate the sample imbalance problem to a certain extent, the traditional GAN model suffers from the pattern collapse problem while generating positive samples [15]. Therefore, WGAN [16], a Wasserstein distance-based generative adversarial network, is recommended in the proposed method to alleviate the pattern collapse problem and enlarge the present pulsar dataset. WGAN was first utilized to generate some images that approximate the real pulsar as positive samples and then fuse the generated positive sample images into an unbalanced dataset to train the pulsar recognition model. Experiments proved that training the deep neural network model on the balanced dataset could further improve the model's recognition accuracy. In addition, since the residual network [17–19] is able to overcome the gradient disappearance problem in the deep neural network model, a deep neural network model containing intra-block residual connections and inter-block residual connections was included in the proposed model during the pulsar candidate identification stage. Experiments proved that the module achieved optimal recognition accuracy in all scenarios compared to the shallow deep neural network model.
In this paper, two basic methods utilized in the proposed model are first introduced with detailed figures and illustrations. These basic methods are the generative adversarial network-based pulsar image generation method and the residual network-based pulsar candidate identification method. Then, the HTRU-Medlat dataset is used in the proposed model and the experimental results are obtained; these results indicate that the proposed model achieves the best performance in the experiment without any other complicated data generation method, which is why HTRU-Medlat was chosen as the dataset for the experiment. In the proposed model, a time-versus-phase plot and a frequency-versus-phase plot are used to implement the screening of pulsar candidates and describe their characteristics of pulsar candidates so that samples can be better evaluated. As a result, positive samples can be identified more accurately, which is essential because positive samples represent the essential information of pulsar candidates. After collecting the experimental results, several evaluation indicators, including Precision, Recall and F1-score, are selected to assess our experimental results. Finally, the results of the proposed models are compared with other existing models. The experimental results show that ResNet exhibits a better ability to fit data and extract features on small datasets and large datasets containing images generated by generative adversarial networks compared to CNN methods. In the comparison experiments between the small dataset and the extended large dataset, the improved F1 values and accuracy metrics of the CNN method indicate that the simulated sample-extended data generated by the generative adversarial network can improve the model's accuracy to some extent. Through experimental validation, better results are obtained: the quality of the large dataset extended with simulated samples is improved, providing richer recognition features, and the recognition accuracy is further improved [4].
2. METHODS
In this paper, a framework combining generative adversarial networks and residual networks is proposed for pulsar candidate identification. First, the generative adversarial networks module is used to tackle the imbalance problem in the dataset, and it is able to generate a series of pulsar candidate images that approximate positive samples to expand the existing pulsar dataset. Then, based on the idea of residual connectivity, this paper designs a deep neural network for pulsar candidate identification utilizing intra- and inter-block residual connectivity, which can effectively improve the recognition accuracy.
2.1. Generative adversarial network-based pulsar image generation method
In this paper, the Wasserstein distance [19] is used to replace the Jensen-Shannon (JS) divergence of the traditional GAN [20, 21] because it can more explicitly measure the difference between two different distributions. Wasserstein GAN (WGAN) based on the Wasserstein distance can overcome problems such as the gradient vanishing and mode collapse experienced by the traditional GAN training, and it can generate more stable pulsar images.
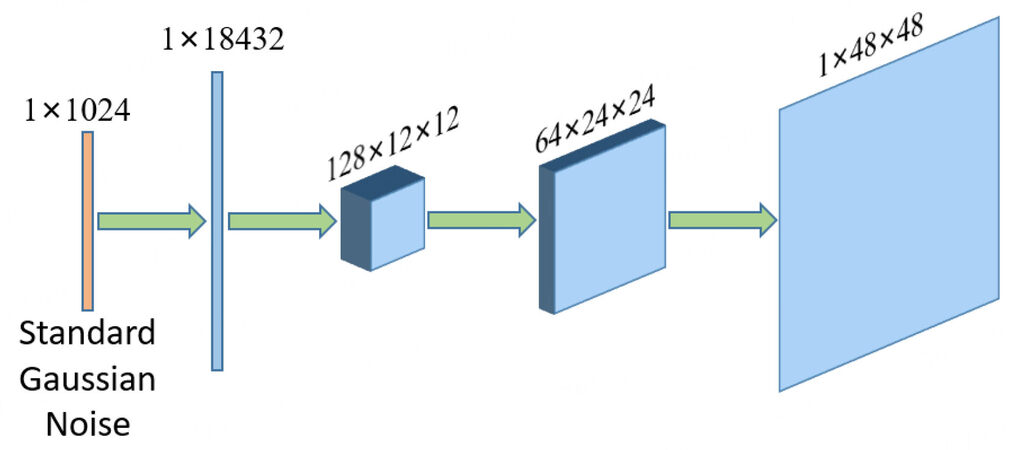
The architecture of the generator is illustrated in Figure 1. The generator produces 1 × 48 × 48 grey images by accepting 1 × 1024-dimensional Gaussian noise as inputs. First, the Gaussian noise is transformed into a 1 × 18432 tensor with a 1024 × 18432 fully connected layer. Then, it is projected and reshaped into a 128 × 12 × 12 tensor with 128 channels. In the next two convolutions, kernels of size 4 × 4 are adopted and the numbers of channels are 64 and 1. The LeakyReLU activation function with a slope of 0.1 is used for all of the convolutions except the last one, and the sigmoid activation function is used in the last convolutional layer to ensure that the pixel values of the final output are in the range [0, 1] to generate appropriate grey images.
Figure 1. Generator architecture. The input is 1 × 1024-dimensional Gaussian noise; that input is first transformed into a 1 × 18432 tensor with a 1024 × 18432 fully connected layer. Then the tensor is projected and reshaped into a 128 × 12 × 12 tensor. There are two convolution layers. The output is a generated 1 × 48 × 48-dimensional grey image.
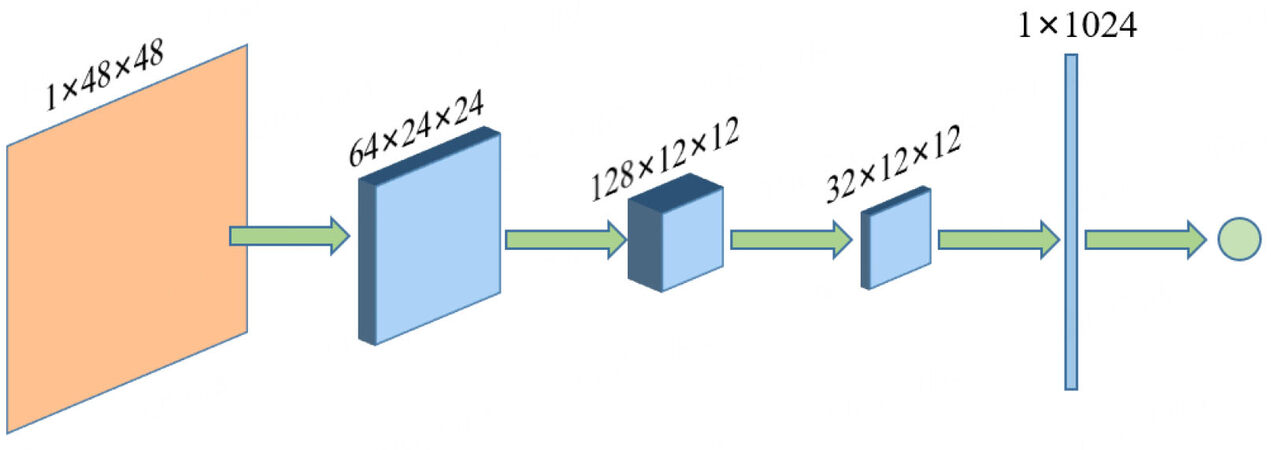
The structure of the discriminator is illustrated in Figure 2. The discriminator designed in this paper accepts 1 × 48 × 48-dimensional grey images as inputs and then obtains the scoring of the corresponding image and calculates the Wasserstein distance between the real data and the simulated data. The first two convolutions use a 4 × 4 convolution kernel, and the last convolution uses a 3 × 3 convolution kernel. There are 64, 128 and 32 channels for these three convolutional layers. After the convolution, the image is reshaped into a two-dimensional tensor, and the image score is calculated with a fully connected layer. The LeakyReLU activation function with a slope of 0.1 is used for all layers except the last fully connected layer. However, the sigmoid activation function is not used in the last layer because the Wasserstein distance is used instead of the original JS distance. It is empirically shown [16] that this model can significantly alleviate the mode collapse problem of the generative adversarial network.
Figure 2. Discriminator architecture. The input samples are 1 × 48 × 48 grey images, and here are three convolution layers. After the convolution, the images are reshaped into 1 × 1024-dimensional tensors.
The generator and discriminator are trained iteratively throughout the training process. The Wasserstein distance between the simulated pulsar sample and the real pulsar sample is optimised iteratively, and the simulated pulsar sample produced by the generator is finally able to accurately characterize the real sample.
2.2. Residual network-based pulsar candidate identification method
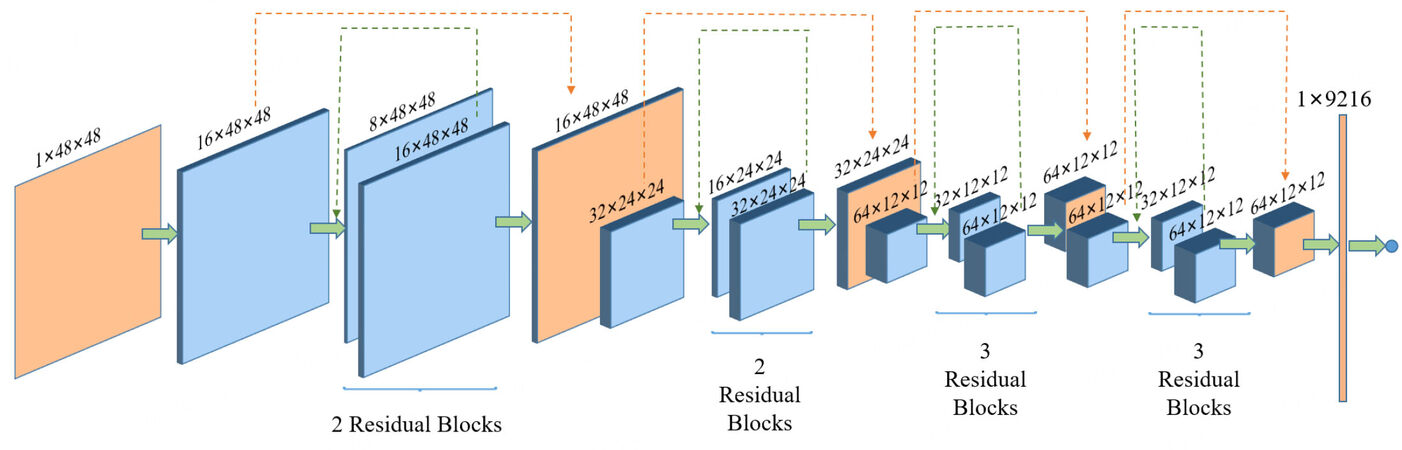
In this paper, a residual network with 24 CNN layers [Figure 3] is designed for pulsar candidate identification. Unlike the original residual network, the proposed residual network has both intra-module residual connections (Figure 3, green dashed line) and inter-module residual connections (Figure 3, red dashed line). The blue colour indicates the convolution process and the orange colour indicates the hidden state. There are four modules in the convolution process, each of which has a stacking number of 2, 2, 3, and 3 layers. A pulsar candidate image of size 1×48×48 is first generated as a 16 × 48 × 48 tensor by the first convolutional layer, which has a convolution kernel size of 3 × 3 and a channel number of 16. The image is then input into the first module; this module first reduces the number of channels to 8, which is then raised to 16 to output a 16×48×48 tensor. That tensor is then input into the same module again with non-shared parameters. At the end of the first module, the final output is added to the input tensor of the same dimension before the first module to obtain a 16 × 48 × 48 orange tensor as the input to the next module [Figure 3]. Therefore, repeatedly, after four modules that employ the convolution operation, the final output feature map is a 1 × 9216 tensor, which is used for future identifications.
Figure 3. An illustration of the pulsar identification model. The blue colour indicates the convolution process, and the orange colour indicates the hidden state. The green dashed line indicates the intra-module residual connections, and the red dashed line indicates the inter-module residual connections. The inputs are the 1 × 48 × 48 grey images. There are four modules, and the outputs are 1 × 9216 features.
3. RESULTS
3.1. Datasets and evaluation indicators
The pulsar candidate dataset used for the experiments is HTRU-Medlat, which is first publicly available labelled pulsar dataset published by Morello et al[6]. The dataset is a collection of labelled pulsar candidates from the intermediate galactic latitude part of the HTRU survey, and it contains exactly 1, 196 positive samples from 521 distinct sources and 89, 996 negative candidates. In addition, the HTRU-Medlat dataset contains both temporal phase (ints) images and frequency phase (bands) images. The evaluation indicators used in the pulsar candidate identification problem are: Precision, Recall and F1-score. Table 1 shows the confusion matrix for the binary classification problem, which classifies all possible predictions in that problem.
Confusion matrix of the dichotomous problem
| Predicted class:Negative (N) | Predicted class:Positive (P) | |
| Actual class: True (T) | TN | TP |
| Actual class: False (F) | FN | FP |
The assessment indicators used in this paper can be obtained by using a dichotomous confusion matrix.
(1) Accuracy rate: the proportion of samples with positive predictions that are correctly predicted, i.e.,:
(2) Recall: the proportion of all samples with positive true labels that are correctly predicted to be positive, i.e.,:
(3) F1-score: the combined accuracy and recall is the F1-score, i.e.,:
3.2. Model comparison experiment
The proposed model uses a CNN[7] model for comparison, which has a similar structure to the LeNet network structure[22], but with some adaptations for the pulsar candidate identification task. For the hyperparameter settings of the residual network model, this paper uses a mini-batch size of 128, a learning rate of 0.001, a size of 0.00001 for the L2 regularisation term, and a standard Gaussian to initialise the model parameters. In addition, the model employs the ReLU[23] activation function for all layers except the last layer of the model, which uses a sigmoid activation function. The objective function for optimisation is cross-entropy, and the Adam[24] optimiser is used.
For the generative adversarial network's hyperparameter settings, the learning rate is 0.001, the L2 regularization weight is 0.0005, the number of training rounds is 200, the optimiser is Adam, the size of the minibatch is 128, the parameters are initialized using Kaiming initialization[25], the discriminator is trained with 5 rounds for each batch, the discriminator weights range from [-0.005, 0.005], and LeakyReLU employed a slope of 0.1.
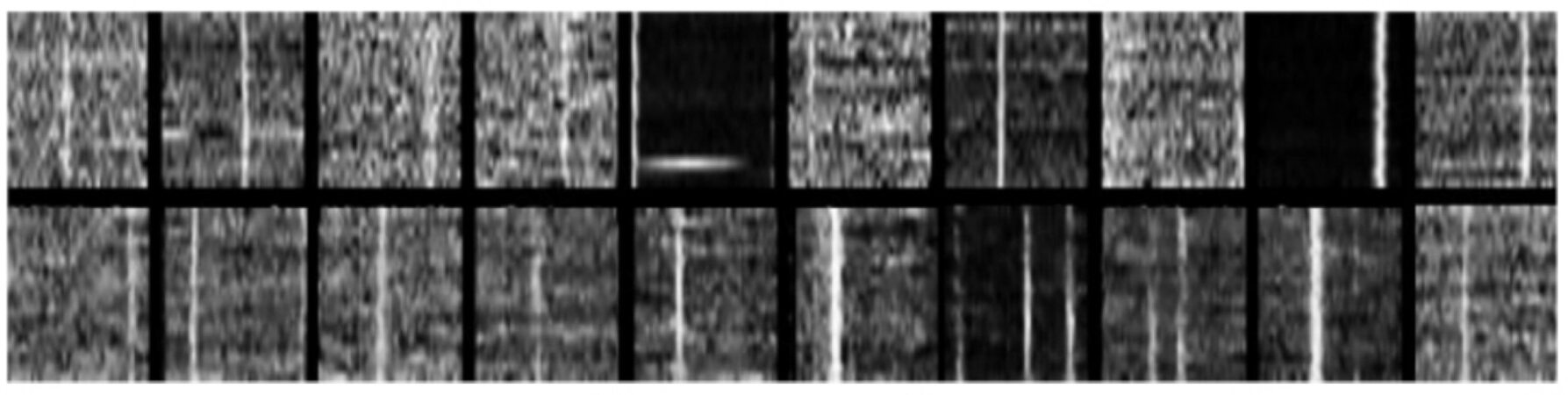
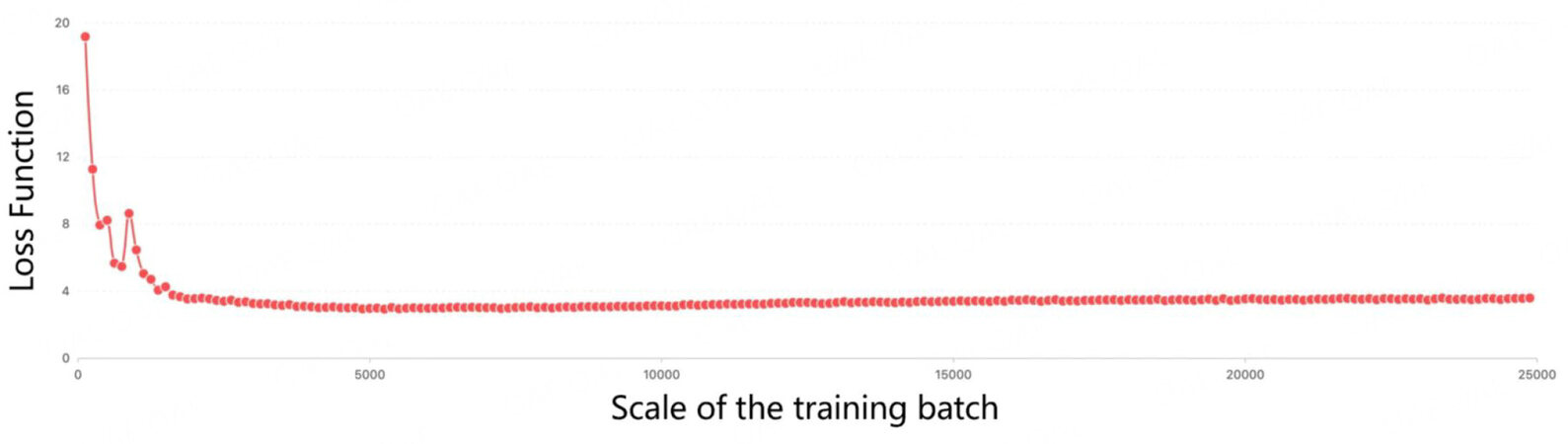
The simulated positive samples generated by the trained generator in this paper are shown in Figure 4, where the ten images in the first row are the real pulsar samples and the ten images in the second row are the simulated samples produced by the generator in this paper. It can be seen that the simulated samples generated by the model can retain the features of the real pulsar samples to a certain extent.The training loss on the HTRU-Medlat dataset is demonstrated in Figure 5, which reveals the optimised training performance of the proposed method in the experiment. The training loss curve declines sharply when the quantity of training samples is relatively small, and the simulated and real pulsar image loss remains fairly low at 4% when the dataset is expanded. The training loss of the proposed method is significantly lower than that of other existing models, thus guaranteeing better performance in pulsar sample identification.
Figure 4. Simulation samples generated based on the generative adoration network (time-phase images of the HTRU-Medlat dataset).
To verify that the generative model can alleviate the problem of sample imbalance, we divide the dataset into two cases, one is an imbalanced data scenario (IDS) with 696 real samples and 10, 000 fake samples, and the other is a balanced data scenario (BDS) with 10, 000 real samples and 10, 000 fake samples. For the HTRU-Medlat dataset, the detailed partitioning scenarios are shown in Table 2.
HTRU-Medlat dataset partitioning after expansion
| Sample size | of real samples | of fake samples |
| Total number of samples in the original dataset | 1, 196 | 89, 996 |
| IDS training set size | 696 | 10, 000 |
| BDS training set size | 10, 000 | 10, 000 |
| Test set size | 500 | 500 |
This paper uses a CNN [7] model for comparison, which has a similar structure to the LeNet network structure [22], but with some adaptations for the pulsar candidate identification task. For the hyperparameter settings of the residual network model, this paper uses a mini-batch size of 128, a learning rate of 0.001, and a size of 0.00001 for the L2 regularisation term used. We also used a standard Gaussian to initialise the parameters of the model and a ReLU [23] activation function for all layers except the last layer of the model, which uses a sigmoid activation function. The objective function for optimisation is cross-entropy, and the Adam [24] optimiser is used.
For the hyperparameter settings of the generative adversarial network, the learning rate is 0.001, the L2 regularization weight is 0.0005, the number of training rounds is 200, the optimizer is Adam, the size of the minibatch is 128, the parameters are initialized using Kaiming initialization [25], the discriminator is trained with 5 rounds for each batch, the discriminator weights range from [-0.005, 0.005], and LeakyReLU employed a slope of 0.1.
The simulated samples are generated using the generative model based on the generative adversarial networks designed in this paper. During the training process, real samples from the IDS training set are used for training. The trained model is then used to generate a series of simulated samples that are used to augment the real sample data. In addition, the simulated samples are filtered, i.e., the generated simulated samples need to be identified as positive by the corresponding residual network model proposed in this paper. The filtered simulated samples are used to expand the IDS training set to obtain the BDS training set.
The results of the automatic identification of pulsar candidates for each method on the HTRU-Medlat dataset are shown in Table 3. "Subints" indicates that the temporal phase images were input, and "Subbands" indicates that the frequency phase images were input. The method with "IDS" indicates that the experiment was tested with small data, while "BDS" indicates that a large dataset consisting of images generated by a generative adversarial network was incorporated. In the IDS data set scenario, the F1 value of the CNN model method reached approximately 95%, while the F1 value of the ResNet method proposed in this paper reached 97.3% and 97.5% in the ints and bands scenarios respectively, which indicates that the ResNet method is able to fit the data better than the CNN method, and can extract features with more classification ability on a smaller dataset. In addition, when using the BDS method, both models incorporate the simulated samples generated by the generative adversarial network. It can be seen that for the ints and bands images, the CNN method improves the F1 value by 1.3% and 1.5% on the BDS scenarios compared to the IDS scenarios, and the precision metric improves by 3.6% and 3.7% compared to the IDS scenario. In addition, it can be seen that for the ints and bands images, the ResNet method improves Recall by 1.6% and 1.7% for the BDS scenario compared to the IDS scenario, and the F1 values improve by 0.9% and 0.8% compared to the IDS scenario. These results indicate that the data expanded by the simulated samples generated by the generative adversarial network are of higher quality and can provide richer recognition features, which causes the model's recognition to be more accurate to a certain extent.
Results of GAN-based generated images on the HTRU-Medlat dataset
| Model & Dataset | F1-score | Recall | Precision |
| CNN | |||
| Subints (IDS) | 95.6% | 94.8% | 96.3% |
| Subints (BDS) | 96.9% | 94.0% | 99.9% |
| Subbands (IDS) | 95.8% | 95.4% | 96.2% |
| Subbands (BDS) | 97.3% | 94.8% | 99.9% |
| ResNet | |||
| Subints (IDS) | 97.3% | 96.4% | 98.3% |
| Subints (BDS) | 98.2% | 98.0% | 98.4% |
| Subbands (IDS) | 97.5% | 95.7% | 99.3% |
| Subbands (BDS) | 98.3% | 97.4% | 99.3% |
Different pulsar candidate identification methods are contrasted respectively, as shown in Table 4. For the traditional methods, manual experts review the pulsar candidates slowly, and thus, the models are evidently time-consuming. Neural network-based methods have better identification results but suffer from the sample imbalance problem. The traditional GAN model alleviates the sample imbalance problem to a certain extent but suffers from the pattern collapse problem in the process of generating positive samples. Compared with the previous methods, the proposed method alleviates the sample imbalance and pattern collapse problems, and has a faster identification speed and higher identification accuracy.
Comparison of the effects of different pulsar candidate identification methods
| Model | Literature | Disadvantage/Advantage |
| Traditional | Eatough RP, Molkenthin N, Kramer M, Noutsos A, Keith M, et al. Selection of radio pulsar candidates using artificial neural networks. Monthly Notices of the Royal Astronomical Society 2010;407:2443–50. [DOI: 10.1111/j.1365-2966.2010.17082.x] | Time-consuming |
| ANN/CNN | Bates S, Bailes M, Barsdell B, Bhat N, Burgay M, et al. The high time resolution universe pulsar survey—Ⅵ. An artificial neural network and timing of 75 pulsars. Monthly Notices of the Royal Astronomical Society 2012;427:1052–65. [DOI: 10.1111/j.1365-2966.2012.22042.x] | Sample imbalance, poor classification |
| Morello V, Barr E, Bailes M, Flynn C, Keane E, et al. SPINN: a straightforward machine learning solution to the pulsar candidate selection problem. Monthly Notices of the Royal Astronomical Society 2014;443:1651–62. [DOI: 10.1093/ mnras/stu1188] | ||
| Zhu W, Berndsen A, Madsen E, Tan M, Stairs I, et al. Searching for pulsars using image pattern recognition. The Astrophysical Journal 2014;781:117. [DOI: 10.1088/0004-637x/781/2/117] | ||
| Lyon RJ, Stappers B, Cooper S, Brooke JM, Knowles JD. Fifty years of pulsar candidate selection: from simple filters to a new principled real-time classification approach. Monthly Notices of the Royal Astronomical Society 2016;459:1104–23. [DOI: 10.1093/mnras/stw656] | ||
| GAN | Guo P, Duan F, Wang P, Yao Y, Yin Q, et al. Pulsar candidate classification using generative adversary networks. Monthly Notices of the Royal Astronomical Society 2019;490:5424–39. [DOI: 10.1093/mnras/stz2975] | Pattern collapse |
| The proposed model | Alleviates sample imbalance problem, improves the accuracy of recognition |
4. CONCLUSIONS
In this paper, a generative adversarial network-based pulsar positive sample generation method is proposed for high-quality sample generation in light of the sample imbalance problem in pulsar candidate identification tasks. Training is performed on a dataset containing only positive samples, and the converged model is used to generate a series of high-quality samples to expand the dataset. A residual network-based pulsar candidate identification method is proposed, and it has a better fitting ability compared to shallow neural network models. Comparison experiments have been conducted with recent pulsar identification methods on the HTRU dataset[26], and the experimental results demonstrated that the proposed method achieved optimal results on the dataset compared to the CNN method.
DECLARATIONS
Authors' contributions
Made significant contributions to the conception and experiments: Yin Q, Liu G, Zheng X
Made significant contributions to the writing: Bao Z, Li Y
Made substantial contributions to the revision and translation: Xie Y, Xu Y, Zhang Z
Availability of data and materials
The data underlying this article are available at http://astronomy.swin.edu.au/~vmorello.
Financial support and sponsorship
The research work described in this paper was supported by the Joint Research Fund in Astronomy (U2031136) under cooperative agreement between the NSFC and CAS and the National Key Research and Development Program of China (No. 2018AAA0100203).
Conflicts of interest
All authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Personalname=Teoh A. The ATNF Pulsar Database. Available from http://astronomy.swin.edu.au/~vmorello/.
2. Keith MJ, Jameson A, Van Straten W, et al. The High Time Resolution Universe Pulsar Survey - Ⅰ. System configuration and initial discoveries. Monthly Notices of the Royal Astronomical Society 2010;409:619-27.
3. Eatough RP, Molkenthin N, Kramer M, et al. Selection of radio pulsar candidates using artificial neural networks. Monthly Notices of the Royal Astronomical Society 2010;407:2443-50.
4. Shamsolmoali P, Chanussot J, Zareapoor M, Zhou H, Yang J. Multipatch feature pyramid network for weakly supervised object detection in optical remote sensing images. IEEE Trans Geosci Remote Sensing 2022;60:1-13.
5. Bates S, Bailes M, Barsdell B, et al. The high time resolution universe pulsar survey—Ⅵ. An artificial neural network and timing of 75 pulsars. Monthly Notices of the Royal Astronomical Society 2012;427:1052-65.
6. Morello V, Barr E, Bailes M, et al. SPINN: a straightforward machine learning solution to the pulsar candidate selection problem. Monthly Notices of the Royal Astronomical Society 2014;443:1651-62.
7. Zhu W, Berndsen A, Madsen E, et al. Searching for pulsars using image pattern recognition. ApJ 2014;781:117.
8. Lyon RJ, Stappers B, Cooper S, Brooke JM, Knowles JD. Fifty years of pulsar candidate selection: from simple filters to a new principled real-time classification approach. Monthly Notices of the Royal Astronomical Society 2016;459:1104-23.
9. Lyon RJ, Brooke J, Knowles JD, Stappers BW. A study on classification in imbalanced and partially-labelled data streams. In: 2013 IEEE International Conference on Systems, Man, and Cybernetics. IEEE; 2013. pp. 1506–11.
10. Hewish A, Bell SJ, Pilkington JD, Scott PF, Collins RA. 74. Observation of a Rapidly Pulsating Radio Source. In: A Source Book in Astronomy and Astrophysics, 1900–1975. Boston: Harvard University Press; 2013. pp. 498–504.
11. Lyon RJ, Brooke J, Knowles JD, Stappers BW. Hellinger distance trees for imbalanced streams. In: 2014 22nd International Conference on Pattern Recognition. IEEE; 2014. pp. 1969–74.
12. Shamsolmoali P, Zareapoor M, Granger E, et al. Image synthesis with adversarial networks: a comprehensive survey and case studies. Inform Fusion 2021;72:126-46.
13. Guo P, Duan F, Wang P, et al. Pulsar candidate classification using generative adversary networks. Monthly Notices of the Royal Astronomical Society 2019;490:5424-39.
14. Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv: 151106434 2015.
15. Zhang CJ, Shang ZH, Chen WM, Xie L, Miao XH. A review of research on pulsar candidate recognition based on machine learning. Pro Compu Sci 2020;166:534-38.
16. Arjovsky M, Chintala S, Bottou L. Wasserstein generative adversarial networks. In: International conference on machine learning. PMLR; 2017. pp. 214–23.
17. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition; 2016. pp. 770–78.
18. He K, Zhang X, Ren S, Sun J. Identity mappings in deep residual networks. In: European conference on computer vision. Berlin: Springer; 2016. pp. 630–45.
19. Bousquet O, Gelly S, Tolstikhin I, Simon-Gabriel CJ, Schoelkopf B. From optimal transport to generative modeling: the VEGAN cookbook. arXiv preprint arXiv: 170507642 2017.
20. Goodfellow I, Pouget-abadie J, Mirza M, et al. Generative adversarial networks. Commun ACM 2020;63:139-44.
21. Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. Computer ence 2015.
22. LeCun Y, Boser B, Denker JS, et al. Backpropagation applied to handwritten zip code recognition. Neural Computation 1989;1:541-51.
24. Kingma DP, Ba J. Adam: a method for stochastic optimization. arXiv preprint arXiv: 14126980 2014.
25. He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In: Proceedings of the IEEE International Conference on Computer Vision; 2015. pp. 1026–34.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Bao Z, Liu G, Li Y, Xie Y, Xu Y, Zhang Z, Yin Q, Zheng X. Pulsar identification based on generative adversarial network and residual network. Complex Eng Syst 2022;2:16. http://dx.doi.org/10.20517/ces.2022.30
AMA Style
Bao Z, Liu G, Li Y, Xie Y, Xu Y, Zhang Z, Yin Q, Zheng X. Pulsar identification based on generative adversarial network and residual network. Complex Engineering Systems. 2022; 2(4): 16. http://dx.doi.org/10.20517/ces.2022.30
Chicago/Turabian Style
Bao, Zelun, Guiru Liu, Yefan Li, Yanxi Xie, Yang Xu, Zifeng Zhang, Qian Yin, Xin Zheng. 2022. "Pulsar identification based on generative adversarial network and residual network" Complex Engineering Systems. 2, no.4: 16. http://dx.doi.org/10.20517/ces.2022.30
ACS Style
Bao, Z.; Liu G.; Li Y.; Xie Y.; Xu Y.; Zhang Z.; Yin Q.; Zheng X. Pulsar identification based on generative adversarial network and residual network. Complex. Eng. Syst. 2022, 2, 16. http://dx.doi.org/10.20517/ces.2022.30
About This Article
Copyright
Data & Comments
Data
 Cite This Article 24 clicks
Cite This Article 24 clicks












Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.