Stability analysis for highly nonlinear switched stochastic systems with time-varying delays
Abstract
In this paper, we examine the stability of highly nonlinear switched stochastic systems (SSSs) with time-varying delays, where the switching time instants are deterministic rather than stochastic. Herein, the boundedness of the global solution is first proven for highly nonlinear SSSs via the average dwell time (ADT) method and multiple Lyapunov function (MLF) approach. Then, the stability criteria for qth moment exponential stability and almost surely exponential stability are presented. The main difficulty lies in the presence of switching and time-varying delay terms, which prevents the validation of existing methods. New inequality techniques have been developed to counteract the effects of switching signals and time-varying delays. Finally, an example is provided to verify the effectiveness of the results.
Keywords
1. INTRODUCTION
Switched systems are important dynamic systems. The idea of switching has been widely applied in various fields, such as aircraft attitude control [1], ecological dynamics [2], and financial markets [3]. With the increasing complexity of system architectures, dynamical analysis of switched systems has attracted significant academic interest. A switched system consists of a family of continuous-time dynamics, discrete-time dynamics, and switching rules between subsystems. According to the switching signal features, switched systems are divided into two categories, {namely}, deterministic switched systems and randomly switched systems. Many researchers have focused on stabilization and stability analyses of various switched systems. For example, in [4], a series of results on stochastic differential equations (SDEs) with Markovian switching was obtained. In particular, the authors have provided some useful stability criteria. In [5], the authors studied the input-to-state stability of time-varying switched systems by employing the ADT method coupled with the MLF approach. The authors of [6] investigated the stability of switched stochastic delay neural networks with all unstable subsystems based on discretized Lyapunov-Krasovskii functions (DLKFs). In [7], a novel Lyapunov function was designed to ensure a non-weighted
The linear growth condition (LGC) is crucial for ensuring the existence of a global solution for a stochastic system. However, many stochastic systems do not satisfy LGC. Hence, the solution of a stochastic system may explode in a finite time. Recently, the stability of stochastic systems without LGC has drawn considerable attention. For instance, the authors of [12] investigated the stability and boundedness of nonlinear hybrid stochastic differential delay equations without LGC based on a Lyapunov function approach. By introducing a polynomial growth condition (PGC), [13] discussed the stabilization problem of highly nonlinear hybrid SDEs. The input-to-state practically exponential stability in the sense of mean square was introduced in [14]. Sufficient conditions for stability have been obtained. Additionally, other meaningful results were reported in [15] and [16].
Time-delay is an important factor that affects dynamical performances of stochastic systems. By constructing a suitable Lyapunov function, the authors of [12] studied the stability and boundedness of highly nonlinear hybrid stochastic systems with a time delay. The authors of [17] used the ADT method to study the stability problem of SSSs, where the switching signals are deterministic. Based on the stability criteria for stochastic time-delay systems, the authors of [18] introduced a suitable Lyapunov-Krasovskii (L-K) functional, and discussed the global probabilistic asymptotic stability of the closed-loop system. In [19], the Razumikhin approach was presented to study the exponential stability of a class of impulsive stochastic delay differential systems. Using the piecewise dynamic gain method, the authors of [20] studied the global uniform ultimate boundedness of switched linear time-delay systems. Motivated by the aforementioned literature, the stability of highly nonlinear SSSs with time-varying delays is studied in this paper. Figure 1 shows the framework of this paper.
The challenges of this article lie in the following two parts: (1) The time delay studied here is merely a Borel measurable function of time
The main advantages of this paper are as follows:
The remainder of this paper is organized as follows. An introduction of the model and important assumptions are given in Section 2. The existence of a unique global solution and stability analysis are presented in Sections 3. In Section 4, a simulation example is presented to validate our theoretical results. Finally, Section 5 concludes the paper.
Note: In this paper,
2. PRELIMINARIES
Model descriptions and assumptions are introduced in this section. In this study, we analyzed the following highly nonlinear SSS with time-varying delays:
with the initial value:
where
Assumption 1. The time-varying delay
where
Remark 1 Assumption 1 reveals that the time delay in SSS (1) is merely a Borel measurable function of time
The following lemma provides a useful inequality to obtain the stability of the SSS (1) with time-varying delays, and its proof can be found in [16].
Lemma 1[16] Let
The conditions for the existence and uniqueness of global solution are the local Lipschitz condition (LLC) and the LGC (see, e.g., [4, 7, 20, 26]). In this paper, the highly nonlinear SSS (1) generally does not require the LGC. Consequently, we must impose the PGC on it.
Assumption 2. (LLC & PGC) For any real number
for all
where
Assumption 3 Assume that there are two functions
where
Moreover, assume that there exists a constant
Remark 2 The system studied in this research has the property of high nonlinearity. In other words, the LGC is removed from the SSS (1), which makes the considered system more general. Without the LGC, the solution of a stochastic system may explode in a finite time. To ensure the existence of a global solution, a PGC (i.e., condition (6)) is imposed on the SSS (1) (see, e.g., [13, 27, 28]). Therefore, the system (1) we studied obeys the LLC (i.e., condition (5)) and the PGC. By combining the MLF approach and ADT method, we then prove the existence and uniqueness of the global solution.
Before presenting the main results, the definition of ADT is revisited.
Definition 1[28] For a switching signal
where
3. MAIN RESULTS
In this section, we prove the existence of a unique global solution for a highly nonlinear SSS (1) by using the ADT and MLF approaches. Then, both the
Theorem 1 Under Assumptions 1-3, if there exists a constant
Then, for any initial data (2), there exists a unique global solution
Proof. We divide the whole proof into two steps. In step 1, for all
Step 1. For all
where
Clearly,
By Lemma 1, we have
and
Hence,
where
is a finite constant. Applying (10) and (11) from Assumption 3, we can deduce that
Recalling the condition (7), we can get
This implies
We observe that
Letting
Step 2. This section proves the existence of a unique global solution for SSS (1). Let
Clearly,
where
For
Combining (18) and (19), it implies that
For
By mathematical induction, for
It follows from (8) and (21) that
Because
Similar to the proof stated in Part 1, we can derive
where
is finite. Then,
Recalling condition (7), we obtain
This implies
Letting
Using Definition 1, we have that for
where
Therefore, for all
This means that the unique solution
The proof is completed.
Remark 3 To deal with the time-varying delay
We now refer to the equation (25) in the proof of Theorem 1. The following theorem provides sufficient conditions for the
Theorem 2 Under the same conditions as those considered in Theorem 1, the solution of system (1) with the initial value (2) is
Proof. Applying (25) yields
Recalling condition (7), we have
Hence, from (12), we observe that
where
Remark 4 The difficulty of the proof is that the time delay
The following theorem demonstrates that a stronger result can be obtained under proper conditions.
Theorem 3 Let Assumptions 1-3 hold. If
Proof. Let
From condition (6), we have
where
Similarly, we also have
From (28), it follows that
where
By the Doob martingale inequality, it follows that
From the well-known Borel-Cantelli lemma[4], it follows that for almost all
Therefore, for almost all
Then, we can obtain
which is the required assertion in (29). Thus, the proof is completed.
So far, we can conclude that under Assumptions 1-3, system (1) is not only
Remark 5 In general, for a stochastic nonlinear system, the
Remark 6 In this paper, the highly nonlinear SSSs with time-varying delays are considered, in which the switching signal is deterministic and differs from those considered in[13, 16, 29-32]. In the current study on stochastic systems with Markovian switching [13, 16, 29-32],
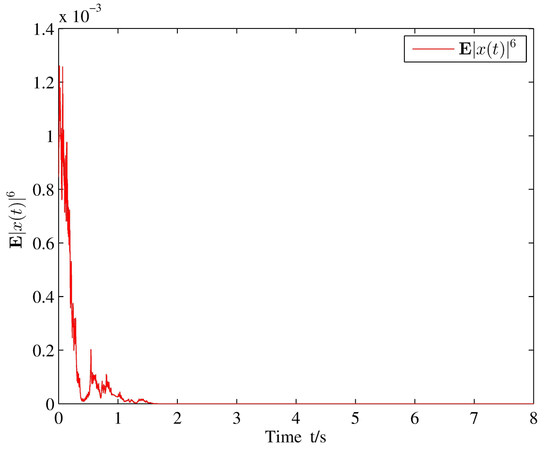
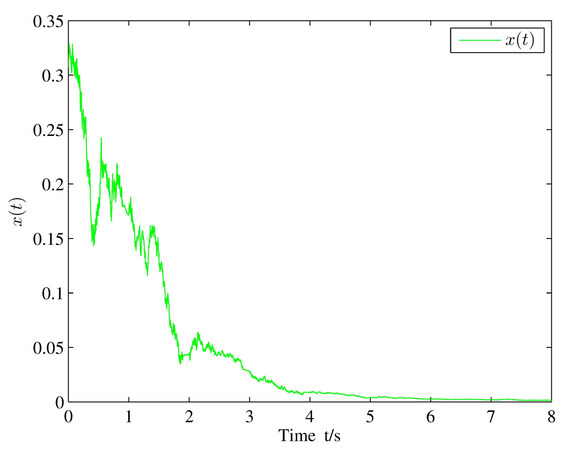
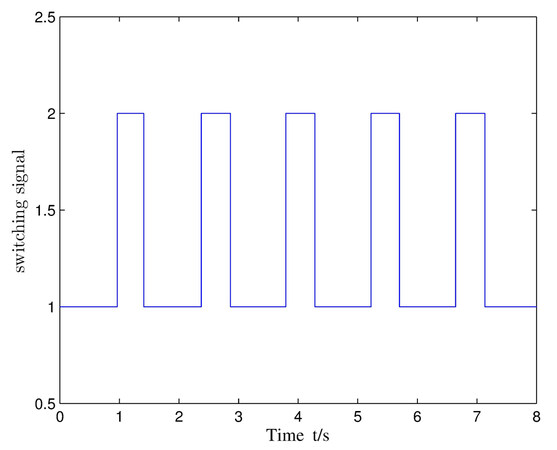
4. NUMERICAL EXAMPLE
In this section, a numerical example is presented to validate the derived results. Consider the following highly nonlinear SSS with a time-varying delay:
where the time-varying delay
In addition, we set
and
Then, we obtain
which means that the condition (9) holds with
5. CONCLUSIONS
In this paper, the existence of a unique global solution for a highly nonlinear SSS with a deterministic switching signal is examined by using the ADT method coupled with the MLF approach. The stability criteria of
DECLARATIONS
Authors' contributions
Made substantial contributions to supervision, writing, review, editing and methodology: Wang H
Performed writing-original draft, software, validation and visualization: Sun J
Availability of data and materials
Not applicable.
Financial support and sponsorship
This work was jointly supported by the National Natural Science Foundation of China (62003170), and the Natural Science Foundation of Jiangsu Province (BK20190770).
Conflicts of interest
All authors declared there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
REFERENCES
1. Zhang R, Quan Q, Cai KY. Attitude control of a quadrotor aircraft subject to a class of time-varying disturbances. IET Control Theory & Applications 2011;5:1140-6.
2. Yoshida T, Jones LE, Ellner SP, Fussmann GF, Hairston NG Jr. Rapid evolution drives ecological dynamics in a predator-prey system. Nature 2003;424:303-6.
3. Preis T, Schneider JJ, Stanley HE. Switching processes in financial markets. Proc Natl Acad Sci U S A 2011;108:7674-8.
4. Mao XR, Yuan CG. Stochastic Differential Equations with Markovian Switching. London: Imperial College Press, 2006.
5. Wu XT, Tang Y, Cao JD. Input-to-state stability of time-varying switched systems with time delay. IEEE Trans Automat Contr 2019;64:2537-44.
6. Xiao HN, Zhu QX, Karimi HR. Stability of stochastic delay switched neural networks with all unstable subsystems: a multiple discretized Lyapunov-Krasovskii functionals method. Inf Sci 2022;582:302-15.
7. Yuan S, Zhang LX, Schutter BD, Baldi S. A novel Lyapunov function for a non-weighted
8. Cheng P, He SP, Luan XL, Liu F. Finite-region asynchronous
9. Wang B, Zhu QX. Stability analysis of Markov switched stochastic differential equations with both stable and unstable subsystems. Systems & Control Letters 2017;105:55-61.
10. Liberzon D. Finite data-rate feedback stabilization of switched and hybrid inear systems. Automatica 2014;50:409.
11. https://doi.org/10.1007/978-0-85729-256-8 [Last accessed on 22 Dec 2022] ]]>.
12. Hu LJ, Mao XR, Shen Y. Stability and boundedness of nonlinear hybrid stochastic differential delay equations. Syst & Contr Let 2013;62:178.
13. Li XY, Mao XR. Stabilisation of highly nonlinear hybrid stochastic differential delay equations by delay feedback control. Automatica 2020;112:108657.
14. Zhu QX. Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Trans Automat Contr 2019;64:3764-71.
15. Zhu QX, Song SY, Shi P. Effect of noise on the solutions of non-linear delay systems. IET Control Theory & Appl 2018;12:1822-9.
16. Dong HL, Mao XR. Advances in stabilization of highly nonlinear hybrid delay systems. Automatica 2022;136:110086.
17. Zhao Y, Wu XT, Gao JD. Stability of highly non-linear switched stochastic systems. IET Control Theory & Applications 2019;13:1940-44.
18. Liu L, Yin S, Zhang LX, Yin XY, Yan HC. Improved results on asymptotic stabilization for stochastic nonlinear time-delay systems with application to a chemical reactor system. IEEE Transactions on Sysems, Man, and Cybernetics: Systems 2016;47:195-204.
19. Hu W, Zhu QX, Karimi HR. Some improved razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans Automat Contr 2019;64:5207-13.
20. Yuan S, Zhang LX, Baldi S. Adaptive stabilization of impulsive switched linear time-delay systems: a piecewise dynamic gain approach. Automatica 2019;103:322-29.
21. Lian J, Feng Z. Passivity analysis and synthesis for a class of discrete-time switched stochastic systems with time-varying delay. Asian J Control 2013;15:501-11.
22. Cong S, Yin LP. Exponential stability conditions for switched linear stochastic systems with time-varying delay. IET Control Theory & Applications 2012;6:2453-59.
23. Yue D, Han QL. Delay-dependent exponential stability of stochastic systems with time-varying delay, nonlinearity, and markovian switching. IEEE Trans Automat Contr 2005;50:217-22.
24. Zeng HB, Liu XG, Wang W. A generalized free-matrix-based integral inequality for stability analysis of time-varying delay systems. Applied Mathematics and Computation 2019;354:1-8.
25. Chen HB, Shi P, Lim CC, Hu P. Exponential stability for neutral stochastic markov systems with time-varying delay and its applications. IEEE Trans Cybernetics 2015;46:1350-62.
26. Mao XR. Stochastic differential equations and applications. Elsevier; 2007.
27. Zhao Y, Zhu QX. Stability of highly nonlinear neutral stochastic delay systems with non-random switching signals. Syst & Contr Let 2022;165:105261.
28. Zhao Y, Zhu QX. Stabilization by delay feedback control for highly nonlinear switched stochastic systems with time delays. Int J Robust Nonlinear Control 2021;31:3070-89.
29. Fei WY, Hu LJ, Mao XR, Shen MX. Structured robust stability and boundedness of nonlinear hybrid delay systems. SIAM J Control Optim 2018;56:2662-89.
30. Shen MX, Fei C, Fei WY, Mao XR. Stabilisation by delay feedback control for highly nonlinear neutral stochastic differential equations. Syst & Contr Let 2020;137:104645.
31. Shen MX, Fei WY, Mao XR, Deng SN. Exponential stability of highly nonlinear neutral pantograph stochastic differential equations. Asian J Control 2020;22:436-48.
32. Song RL, Wang B, Zhu QX. Delay-dependent stability of nonlinear hybrid neutral stochastic differential equations with multiple delays. Int J Robust Nonlinear Control 2021;31:250-67.
33. Kang Y, Zhai DH, Liu GP, Zhao YB, Zhao P. Stability analysis of a class of hybrid stochastic retarded systems under asynchronous switching. IEEE Trans on Automat Contr 2014;59:1511-23.
34. Shen MX, Fei C, Fei WY, Mao XR, Mei CH. Delay-dependent stability of highly nonlinear neutral stochastic functional differential equations. Intl J Robust & Nonlinear 2022;32:9957-76.
35. Ren MF, Zhang QC, Zhang JH. An introductory survey of probability density function control. Syst Sci & Contr Eng 2019;7:158-70.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Sun J, Wang H. Stability analysis for highly nonlinear switched stochastic systems with time-varying delays. Complex Eng Syst 2022;2:17. http://dx.doi.org/10.20517/ces.2022.48
AMA Style
Sun J, Wang H. Stability analysis for highly nonlinear switched stochastic systems with time-varying delays. Complex Engineering Systems. 2022; 2(4): 17. http://dx.doi.org/10.20517/ces.2022.48
Chicago/Turabian Style
Sun, Jing, Hui Wang. 2022. "Stability analysis for highly nonlinear switched stochastic systems with time-varying delays" Complex Engineering Systems. 2, no.4: 17. http://dx.doi.org/10.20517/ces.2022.48
ACS Style
Sun, J.; Wang H. Stability analysis for highly nonlinear switched stochastic systems with time-varying delays. Complex. Eng. Syst. 2022, 2, 17. http://dx.doi.org/10.20517/ces.2022.48
About This Article
Special Issue
Copyright
Data & Comments
Data
 Cite This Article 25 clicks
Cite This Article 25 clicks














Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.